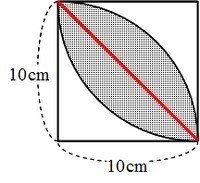
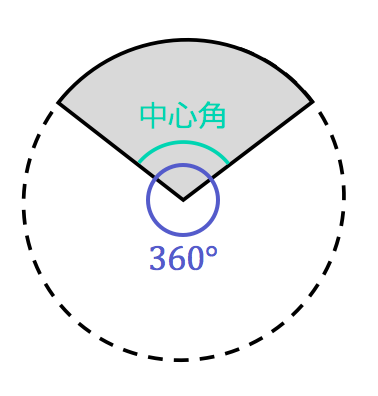
扇形面積＝円の面積×（ 扇の内角／３６０°） 三角形の面積＝（ 半径2×sin扇の内角 ）/２ ・・・二辺夾角法これで、 円の面積がπに半径（ 上の例では、1）の二乗をかけたものであることが 証明できました（変換式のsin、cosの前にrを付ければ、円の面積はπr 2 となる ）。 次に、数値積分の方法を使って円の面積を計算してみます（図2参照）。スポンサーリンク 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率 それでは「円の面積の公式」を使った「練習問題」を解いてみましょう。 練習問題① 半径が 2(cm)の円の面積を求めて
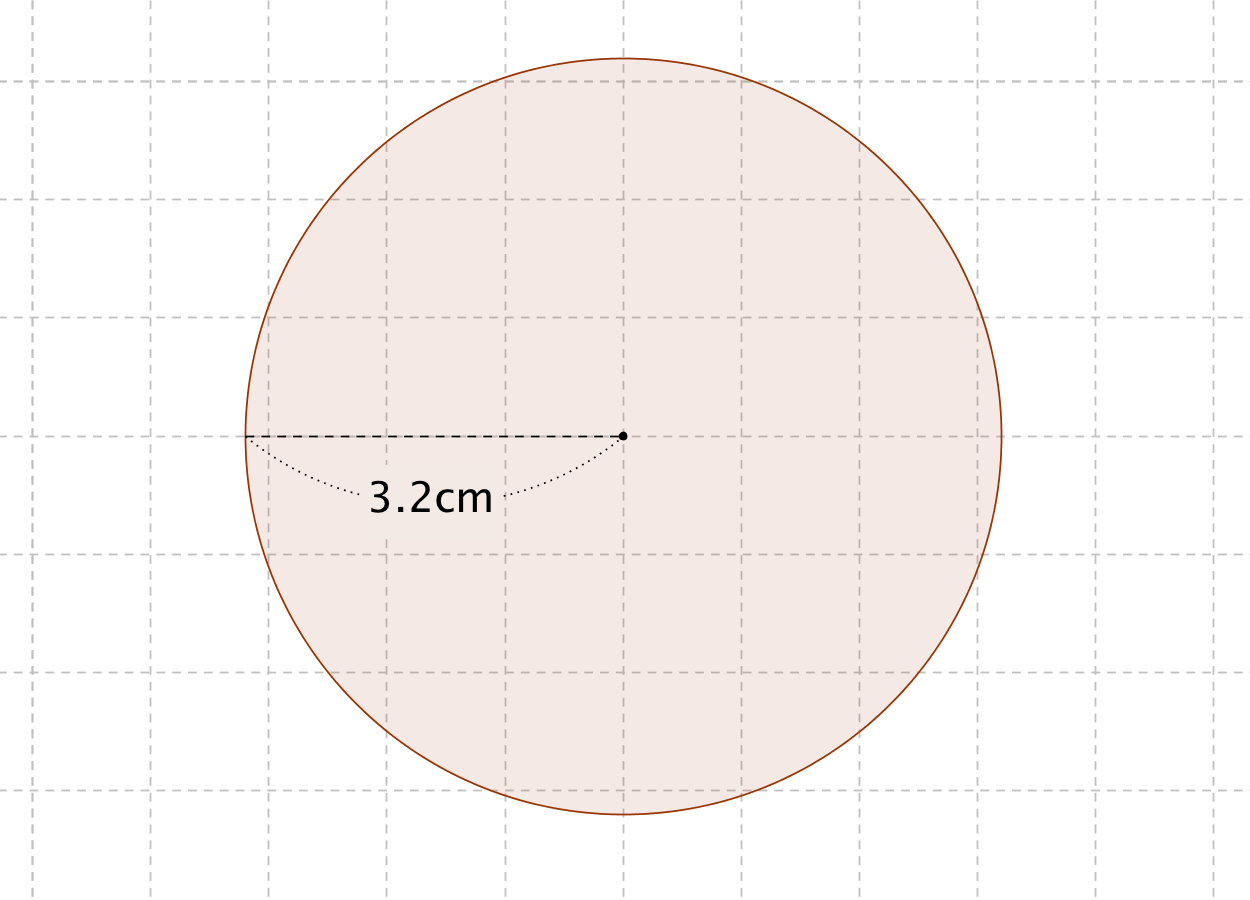
円の面積の公式 算数の公式
中心：原点，半径：r の円の方程式 x 2 y 2 = r 2 r と θ を使って円周上の点Pを表すと， {x円の面積 円の面積は，半径×半径×314で求められます。 この求積公式の指導にあたっては，公式の理解はもとより，そこに至る過程を大切に指導することが重要です。 まず，半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか円と球の公式 \(D\)：直径 \(\rho\)：密度 円の面積 \(\left ( \displaystyle \frac {\pi}{4} \right ) D^2\) 円周 perimeter \(\pi D\) 円形度 circularity （等面積円の円周）／（周長） 球の表面積
世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note
角柱（円柱を含む）や角錐（円錐を含む）の体積の公式は、皆さんにとって周知のものだろう。 当HPでも 四面体の求積 三角錐の体積 円柱の体積 直交する円柱 角錐の体積 ある図形の体積 切断面の高角柱や円柱の体積の求め方を考えている。 技能 角柱や円柱の体積を公式を用いて求めることができる。 知識・理解 必要な部分の長さを用いることで，角柱や円柱の体積は，計算によって求めることができ ることを理解している。公式を用意する 四角柱の場合は V（体積） = 1/2 x (底辺1 底辺2) x 底面の高さ x 角柱の高さ となります。
中学1年生 数学 無料問題集 角柱や円柱の体積 おかわりドリル
単元：おうぎ型の中心角の解き方 問題 半径9㎝、弧の長さが6n㎝のおうぎ形の中心角を求めなさい。 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年～中学3年生内容計算の基礎養成演習時間割 円とおうぎ形 中学受験準備のための学習ドリル Study 円錐の側面 扇形 の中心角の求め方 中2数学 ちくらっぽインク 簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく 数学 円すいの展開図 扇形の中心角は5秒で出せる 受験↓ ↓ ↓ ↓ ↓ ↓https//studyline32com/l/u/6XQOiYkgoDeSmFNm中1で学習する平面図形の単元から「おうぎ形の中心 ★無料の中学メルマガ講座★毎週、問題
3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ
多角形の内角の和は公式がありますので求め方と示す意味を見ておきましょう。 角度を求める問題はいろいろな形で入試でも多く取り上げられますが、 内角の和を使うより外角の和を利用した方が楽な計算になることがありますので、その理 Try IT（トライイット）の高校数学の勉強法の映像 高さが同じ三角形の面積比\ →\ 底辺の比底辺が同じ三角形の面積比\ →\ 高さの比 角が同じ三角形の面積比\ →\ 角を挟む辺の積の比 等高と等底については中学で学習済みであるが,\ について少し補足しておく (相似) 高校生は新たに3の{等角の三角形の直角三角形の左端の角度が30度の時のそれぞれの辺の長さの比を覚えていますか？ 三角形の比についてよくわからない方は、三角比（30°,45°,60°） をみてください。 それでは、sin30°、cos30°、tan30°の求め方を説明していきます。 sin30°の求め方 上の直角
円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
5年生算数「割合」 5年生算数「割合」 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device小学校 5年生 算数 かく力を高める問題 一括ダウンロード 小数のかけ算 問題 合同な図形 問題 図形の角 問題 単位量あたりの大きさ 問題 単位量あたりの大きさ 問題 四角形と三角形の面積 問題 割合 問題 帯グラフと円グラフ 問題 5年生算数割合 小学校5年生 授業「算数」 採用1年目（194~3） 単元中、以下の流れで授業を行うことが多かったです。 復習（黒板の一番左）⇐休み時間中に板書。 めあての確認・問題の確認 まとめ 問題演習
百分率と割合 小学５年生 算数割合 計算プリント Com １ 6年生小学校 算数問題 無料ドリルプリント集
May 22, · 授業時間も増え、学習内容も本格化してくる5年生。家では何をどのくらい勉強させればいいのだろう？と疑問に思う親御さんも多いことでしょう。ここでは、中学受験を目指す5年生の塾のカリキュラムや家庭学習について主任相談員の西村則康が解説しています。/10/5お知らせ新着順に並べなおしました 英語で絵日記をかいてみよう5年英語 冬の言葉でマインドマップをかいてみよう5年生自主学習 円を利用して正多角形をかく方法算数Oct 04, 19 · 小学5年生になると理科の授業で「雲と天気の変化」について学習します。 今回はテスト勉強も踏まえて 自主学習ノート （自学ノート）にまとめることにしました。 なにげなく見ている雲にはそれぞれ名前があることを知ります。
公約数と公倍数の自主学習ノート例 家庭学習レシピ
