多角形の内角の和は公式がありますので求め方と示す意味を見ておきましょう。 角度を求める問題はいろいろな形で入試でも多く取り上げられますが、 内角の和を使うより外角の和を利用した方が楽な計算になることがありますので、その理 Try IT(トライイット)の高校数学の勉強法の映像 高さが同じ三角形の面積比\ →\ 底辺の比底辺が同じ三角形の面積比\ →\ 高さの比 角が同じ三角形の面積比\ →\ 角を挟む辺の積の比 等高と等底については中学で学習済みであるが,\ について少し補足しておく (相似) 高校生は新たに3の{等角の三角形の直角三角形の左端の角度が30度の時のそれぞれの辺の長さの比を覚えていますか? 三角形の比についてよくわからない方は、三角比(30°,45°,60°) をみてください。 それでは、sin30°、cos30°、tan30°の求め方を説明していきます。 sin30°の求め方 上の直角

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
三角形 角度 求め方 高校
三角形 角度 求め方 高校- 三角比の相互関係式 sin 2 A cos 2 A = 1 より、 sin A > 0 であることから、 sin A = √ 1 − cos 2 A これを基本の式に代入すると、 S = 1 2 b c √ 1 − cos 2 A ( ※) また、余弦定理より、 cos A = b 2 c 2 − a 2 2 b c なので、 (※)に代入すると、 ( ※) = 1 2 b c √ 1 − ( b 2 c 2 − a 2 2 b c) 2 あとは式変形を頑張っていきます。 中断 相互関係式を用いれば、 sin A と cos A求角と方程式 角度を求めることは、小学生のころにもやっていることです。 しかし、角度を求めるために方程式を用いることは中学生ならではです。 そんな問題を練習しましょう。 例題1 次の図の角 \(x\) の大きさを求めなさ
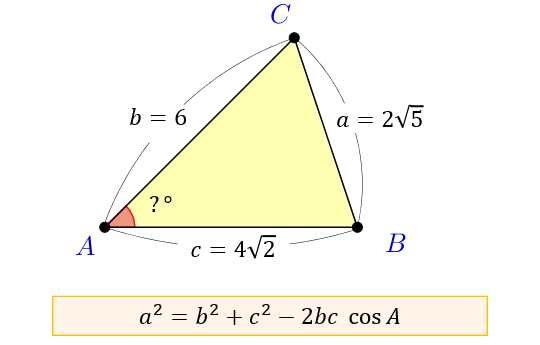



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
例題1 θ が第3象限の角で, cosθ = − 4 5 であるとき, sinθ と tanθ の値を求めましょう。 この問いは,上で導いた 三角関数の相互関係 を用いて式により求める方法と,図を描いて求める方法とがあります。 解答1 cosθ = − 4 5 を sin2θ cos2θ = 1 に代入第48回高さが等しい三角形の面積比①の授業映像は下をクリックしてご覧ください。 中学受験算数・高校受験数学けいたくチャンネル 986K subscribers Subscribe 中学受験算数「高さが等しい三角形の面積比①」小学4年生~6年生対象毎日配信Nhk高校講座 物理基礎 第9回 第1編 物体の運動とエネルギー 力を合わせる 力を分ける ~力の合成と分解~
30°,45°,60°の三角比の値は,今後とても重要になるので,しっかり求められるようにしてください。 そして,その値を利用して解く問題にも対応できるように,いろいろな問題を解いてみましょう。 それでは,これで回答を終わります。 これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。 その他にも苦手なところはありませんか三角比からの角度の求め方3(tanθ) 鈍角を含む三角比の相互関係1(図の利用) 鈍角を含む三角比の相互関係2(公式の利用) 直線の傾きと三角比;このとき角度θにおける三角比を きの点P の座標を求め,三角比を計算 せよ。 (1) r =1のとき P( , ) sin1 = cos1 = tan1 = (2) r =2のとき P( , ) sin1 = cos1 = tan1 = 高知工科大学基礎数学シリーズ3 「三角関数」(改訂版) −7 − < 鈍角の三角比2 > 図1の場合 sinθ= Y r , cosθ= X r , tanθ= Y X である。 問1 θ=150
対頂角は等しいから,右図の緑で示した2つの角 ∠z は等しい. 三角形の内角の和は180°だから 64°°∠x=180° したがって ∠x=34° (答) (別解) 三角形の外角は,それと隣り合わない2つの内角の和に等しいから,右図の黄色で示した外角は2通りに計算でき,どちらで計算しても等しい. ∠x°=56°60° ∠x=34° (答) このとき, b c bc bc と e f ef ef をくっつけてできる三角形 a c d acd a c d は二等辺三角形となる。 よって, ∠ C A D = ∠ C D A \angle CAD =\angle CDA ∠ C A D = ∠ C D A であり,2つの直角三角形は斜辺と1つの直角でない角が等しい。 三角形の面積の求め方に なります。 高校入試でも よく出題されるところなので しっかりと マスターしておきましょう! まとめ 関数のグラフの中にある 三角形の面積を求めるコツ についてまとめます。 ① x軸やy軸に平行な線で 三角形を分割して、 底辺や それぞれの高さを




三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd




三角形の3辺から角度を計算 高精度計算サイト
二等辺三角形の4つの性質と4つの条件 二等辺三角形の角度の求め方と例題 対頂角、同位角、錯角の意味を分かりやすく解説 四角形の内角の和が360°であることの2通りの証明 多角形の内角の和の公式を3通りの方法で証明する 正多角形の内角と外角の大きまずは、角度Bは簡単に求まります。三角形の内角の和は180度ですから、「C = 180 A B = 180 35 90 = 55」より、角Cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみましょう。三角関数の定義から、「a = c sin A = 7×sin35°」、「b = c cos A = 7×cos35°」だと分かりますので、これを計算尺を利用して計算してみましょう。ほかの記事を探す 分野別 レベル別 他 キーワードで検索する 数学の実力を試そう 入試数学コンテスト 物理の記事 高校生から味わう理論物理入門 記事の一覧へ 質問




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
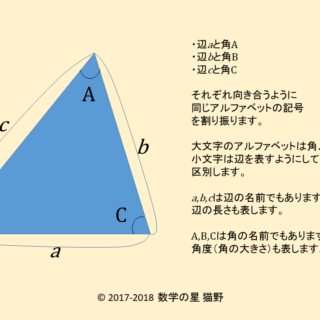
下の四角形のaの角度を求めなさい。 解説 下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 °三角形を表すとき 多くの場合、頂点の名前は A , B , C の順に左回りに付けます。 辺の名前は「向かい合う角」の小文字で表します。 したがって、 A の対辺 BC を a とします。 同様にして、特に断り書きがなければ b=AC , c=AB になります。 頂点の名前 A , B , C でその内角∠ A 、∠ B 、∠ C の大きさを表し、単に sin A , sin B , sin C などと書きます。 例 右図において問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答



3




タンジェントとは何か 中学生でも分かる三角関数の基礎
S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2) i f a ≥ b, c h = 2 S a, B三角形の内角 三角形の内角の和は \(180°\) である。 内角とは、内側の角のことですね。 三角形の \(3\) つの内角の大きさをすべて、足すと \(180°\) 、つまり一直線になるということです。 三角形がど正弦定理から,三角形の辺の長さを求める計算について ABCにおいて a = 3 , A = 60°, B = 45°のとき b を求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりません。 なぜルートが出てくるのですか? (3 ÷√3/2)×1/√2が,もう何




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。 中学数学直角三角形の辺の長さの求め方超丁寧に 中学数学三角柱の体積の求め方と公式5秒でわかる コメントを残す コメントをキャンセル メールアドレスが公開されることはありません。 * が付いている欄は必須項目です コメント 名前 * メールアドレス * サイト 前の記 完全版三角形の面積求め方一覧 中学〜高校までの三角形の面積と面積比についてまとめました。 115 0 恋する数学 教材職人 全統マーク模試やり直し 数学Ⅰ*a 97 3 さき このノートに関連する質問 高校生 数学 2番の答えは39個なんですけどやり方が分からないので教えてほし




力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




角度の求め方を教えてください ちなみに答えは です お願いします Clear
・同経度の2地点間の距離を求めた。 ・"球面三角形は3つの大円の交わりから定義される。" ・(メネラウスの紹介) 1、球面上の「角」 角度について、『球面学』第1巻では以下のように定義している。 (定義)AB、ACを大円の弧、Aにおけるそれぞれの弧の接線AP、 とする。 半径rのとき、BC52°の三角形の辺の比はわかりませんが,sin 52°,cos 52° の値なら計算機に打ち込めばすぐ求められます。 もちろん52°というのは1つの例であって,他のどんな角度でも sin,cosを斜め方向の力に かけ算することで分力を求めることが可能 です。 180^ {\circ} への拡張 最後に、 180^ {\circ} の三角比( \sin, \cos, \tan )を求めましょう。 180^ {\circ} の場合は、 0^ {\circ} のときと考え方は同じです。 0^ {\circ} の場合は、三角形を横線と考えれることを説明しましたね↓ 高校数学(三角比)三角比の求め方




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



三角形の角度を求める 思考力を鍛える数学
なんと、3つの辺の長ささえ分かれば、面積が分かるのです。 「高さ」を測る必要もない、角度を調べる必要もない。 長さを測るものさしが1つあれば、三角形の面積をサクッと求められるのです(図3)。 たとえば、三角形の3つの辺が5mと3mと4mなら、 s = (534)÷2 = 6 s = ( 5 3 4) ÷ 2 = 6 T = √6(6−5)(6−3)(6− 4) = √6×1×3×2 = √36=6 T = 6 ( 6 − 5) ( 6 − 3) ( 6 − 4) = 6 × 1三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。直角三角形で三平方の定理をつかっているから なんだ。 長方形で対角線をひいたら、 2つの三角形にわかれるでしょ?? そのうちの1つの直角三角形をえらぼう。 そいつで、 三平方の定理をつかって対角線の長さを求めるんだ!直角三角形の高さと斜辺から、底辺・角度・面積を計算します




底辺と高さから角度と斜辺を計算 高精度計算サイト
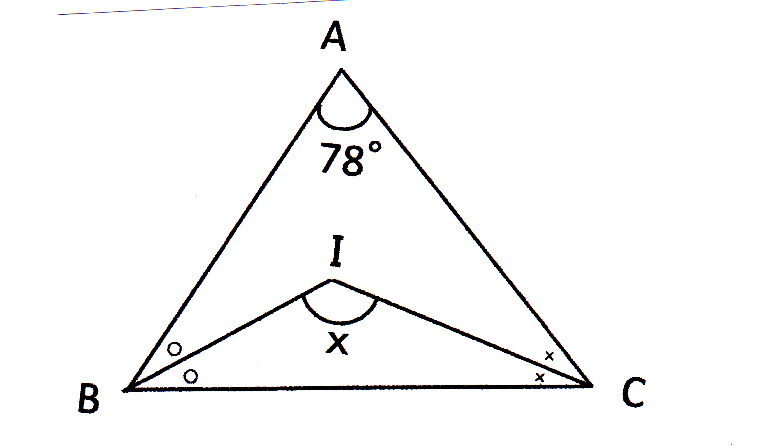



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方




正三角形や二等辺三角形の内角 Youtube




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ
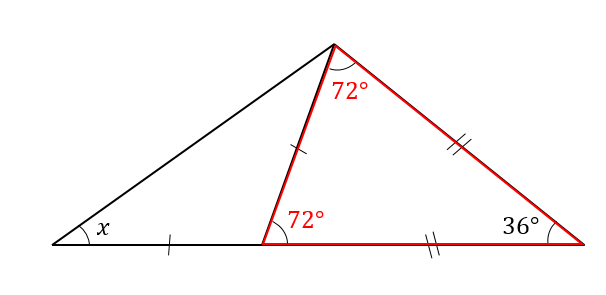



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
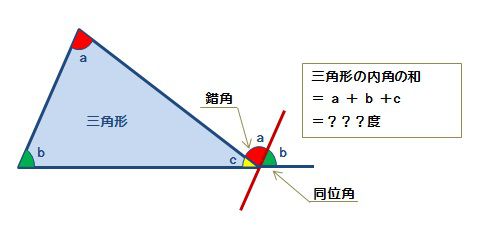



三角形の内角の和 算数の公式覚えてますか
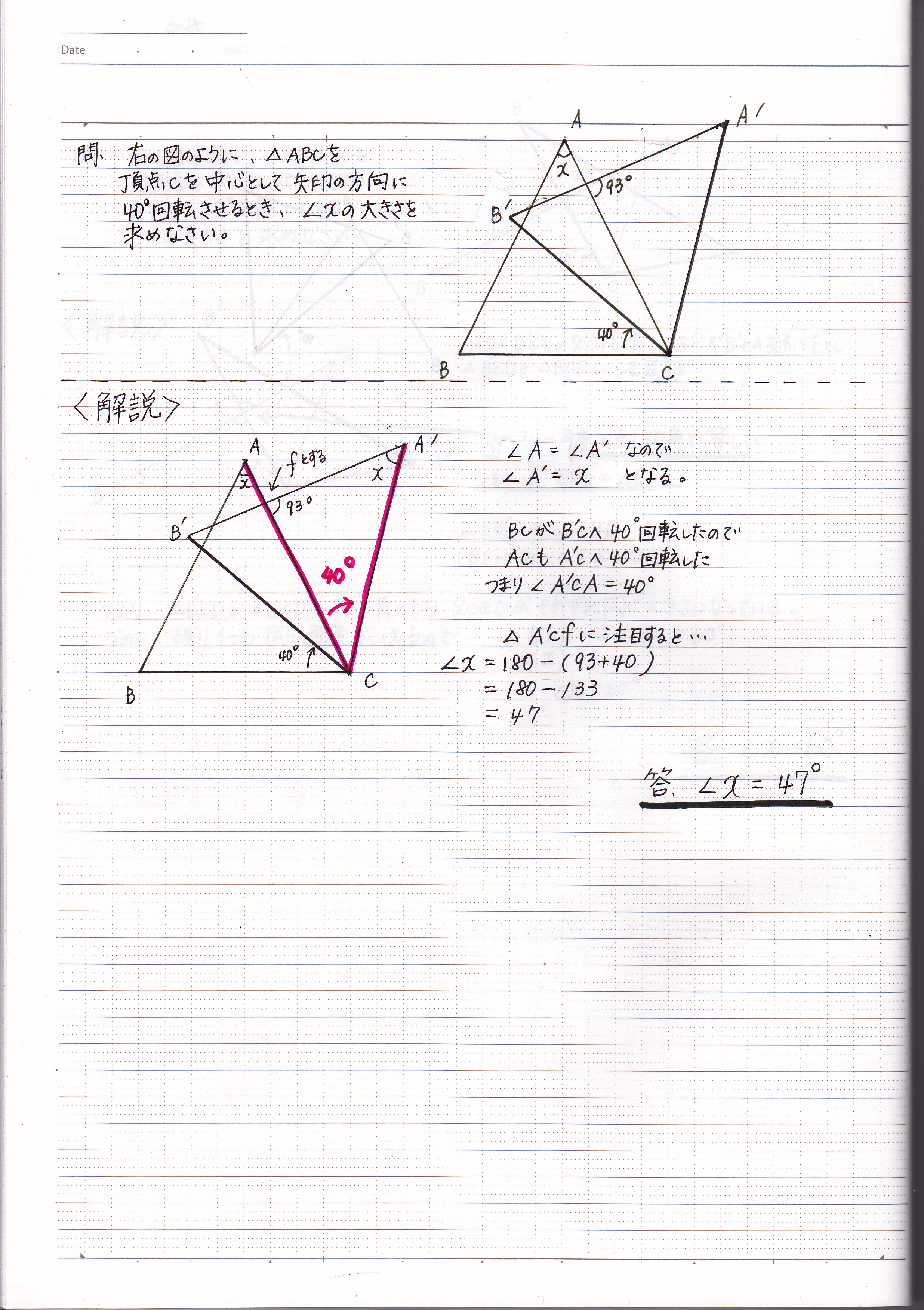



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su



3



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




高校数学a 三角形の内心2 実践 例題編 映像授業のtry It トライイット




三角形の外角と内角の公式 簡単な問題で 外角の求め方を理解しよう 中学や高校の数学の計算問題




余弦定理で角度を求める方法 数学の星




二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思うので教え Clear



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す
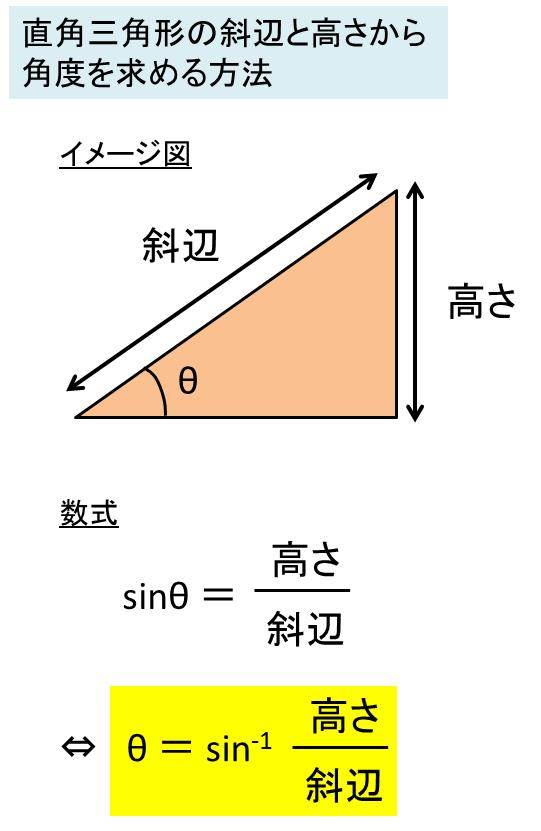



Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算
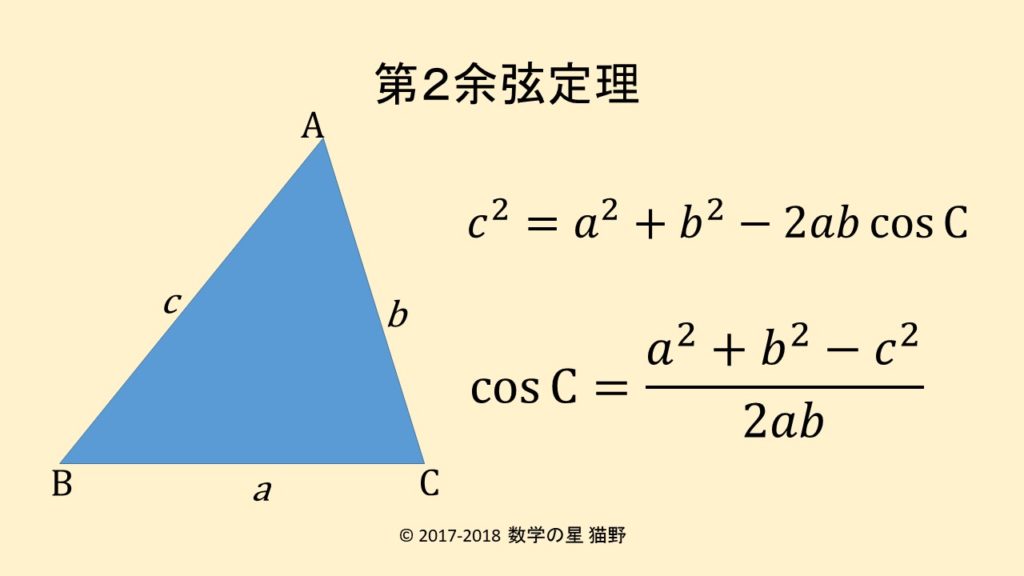



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ



普通の電卓で計算できる直角三角形の近似計算
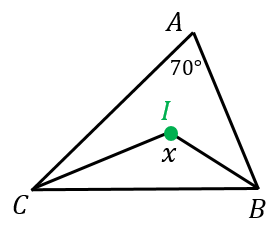



三角形の内心の証明と頻出例題2問 具体例で学ぶ数学




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット
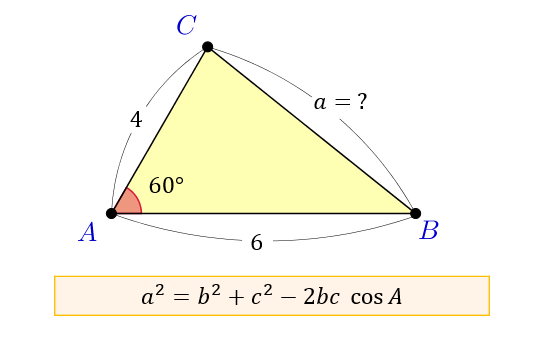



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



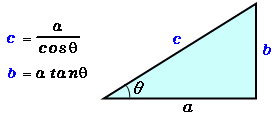
第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星



角度と底辺から斜辺と高さを計算 高精度計算サイト




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




中2 数学 4 2 三角形の角度の利用 Youtube




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
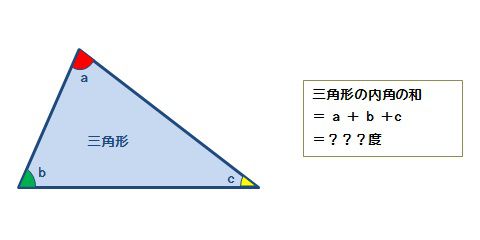



三角形の内角の和 算数の公式覚えてますか



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋




簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく



1




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



1




多角形の内角の和の公式と外角の和を利用した角度の求め方




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




角度の計算 裏技まとめ 教遊者
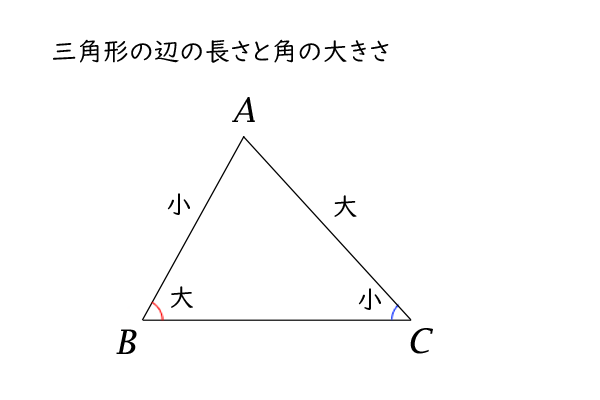



三角形の辺の長さと角の大きさの関係 高校数学マスター



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター




角度の求め方 算数の教え上手 学びの場 Com



2 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に
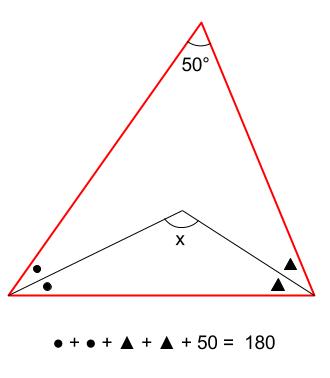



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su
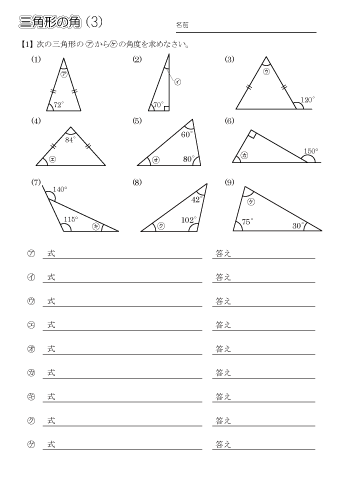



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo
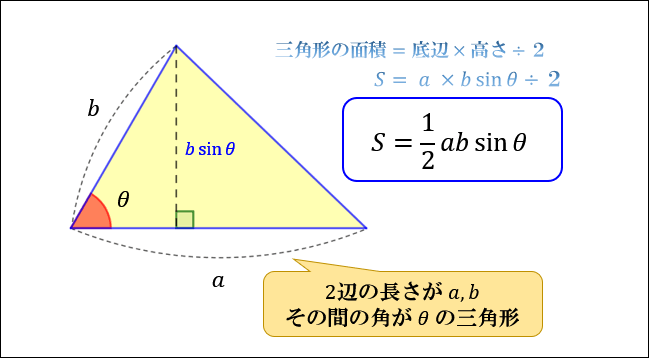



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
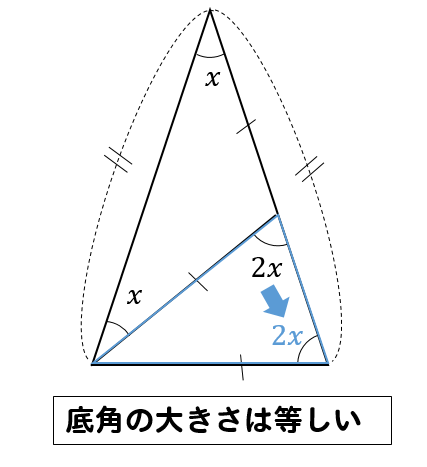



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
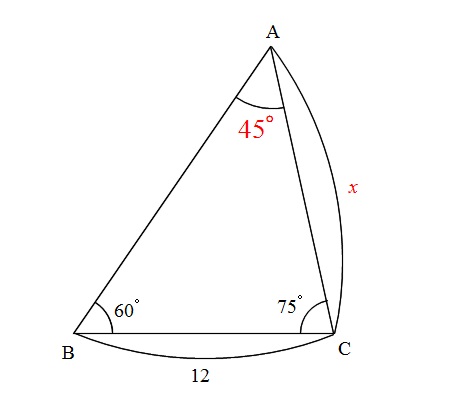



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない




角度の求め方 算数の教え上手 学びの場 Com
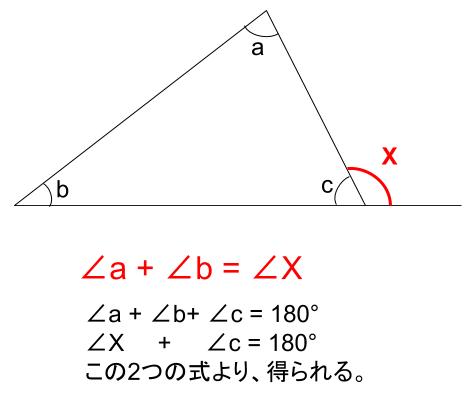



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su
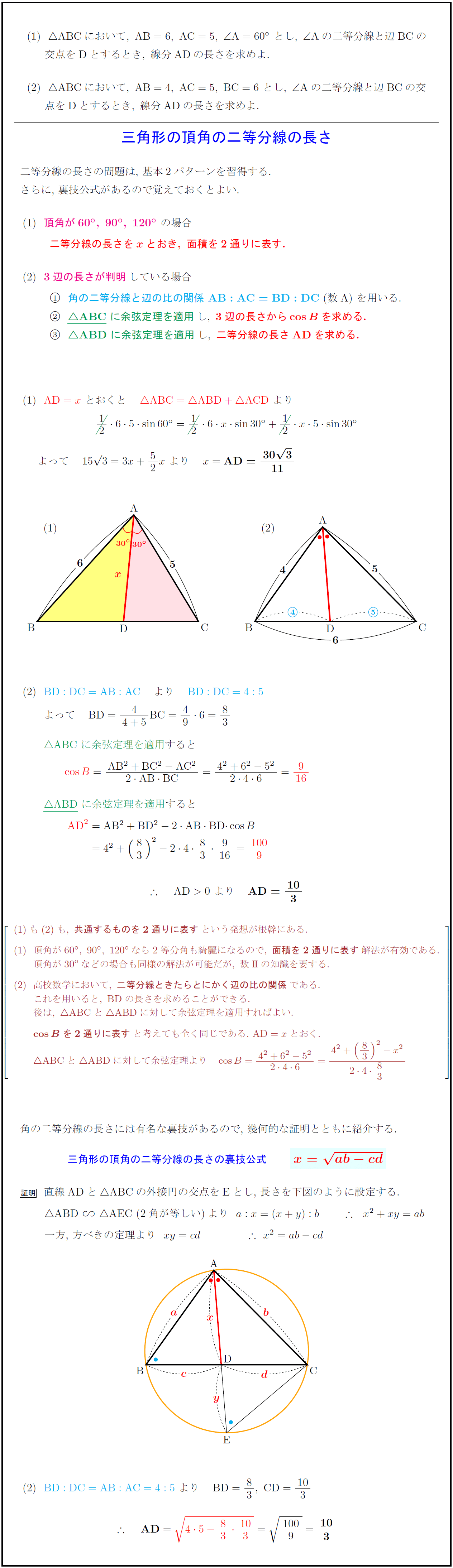



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月
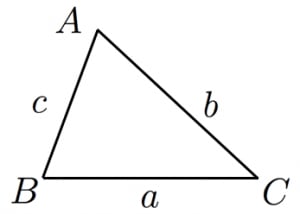



Sinを用いた三角形の面積公式 高校数学の美しい物語




角度の問題まとめ 無料で使える中学学習プリント



外接円とは 半径の公式や求め方 性質 書き方 受験辞典




あ かまでの角度を求めてください 急いでます 教えてください Clear



添付した図のような台形の xの角度を求めようと思っています 参 Yahoo 知恵袋




三角形の外心 高校数学a Youtube
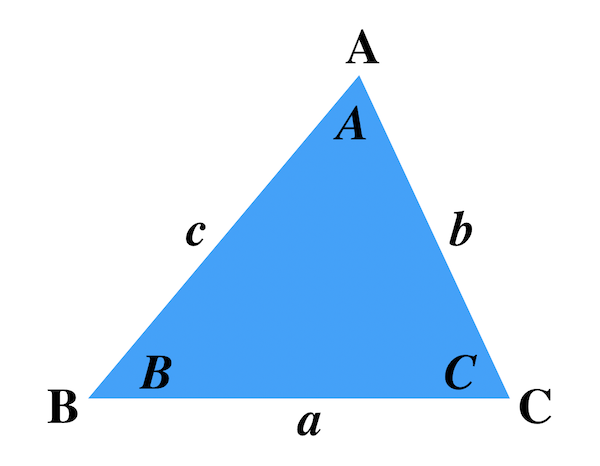



三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




小5 算数 小5 31 三角形の角 Youtube




わかりやすい三角比と基本公式 Irohabook
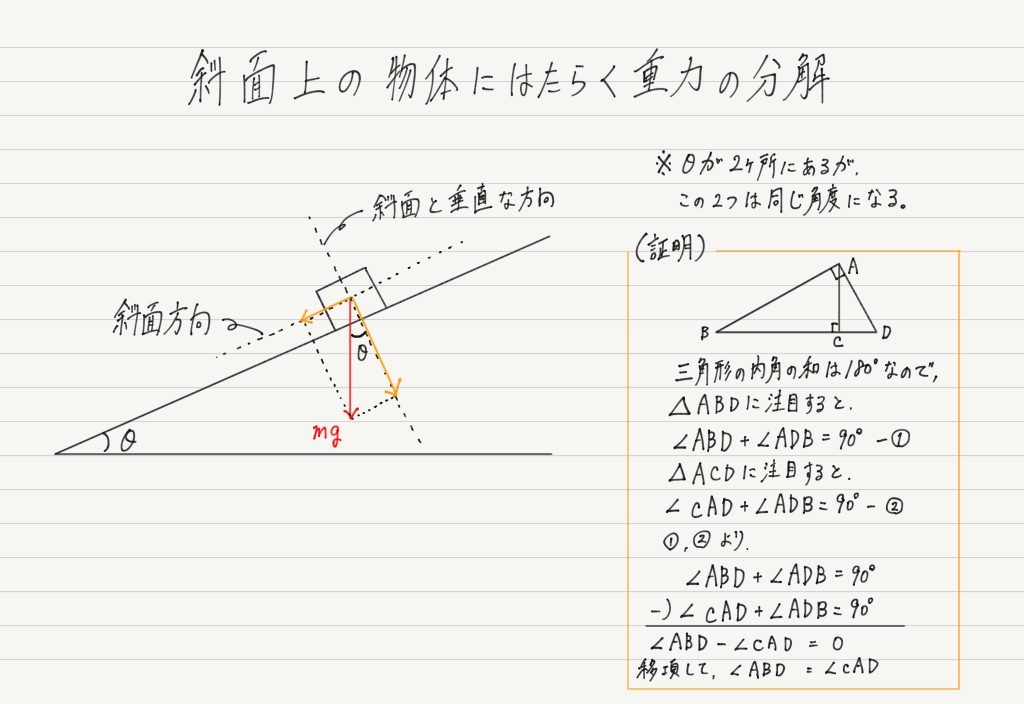



力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
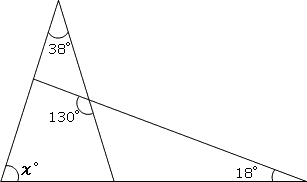



角度の求め方 算数の教え上手 学びの場 Com



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の辺から角度を計算 製品設計知識




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




ちょうちょ型図形の角度は 求め方を徹底解説 数スタ




二等辺三角形の角を求める Youtube




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
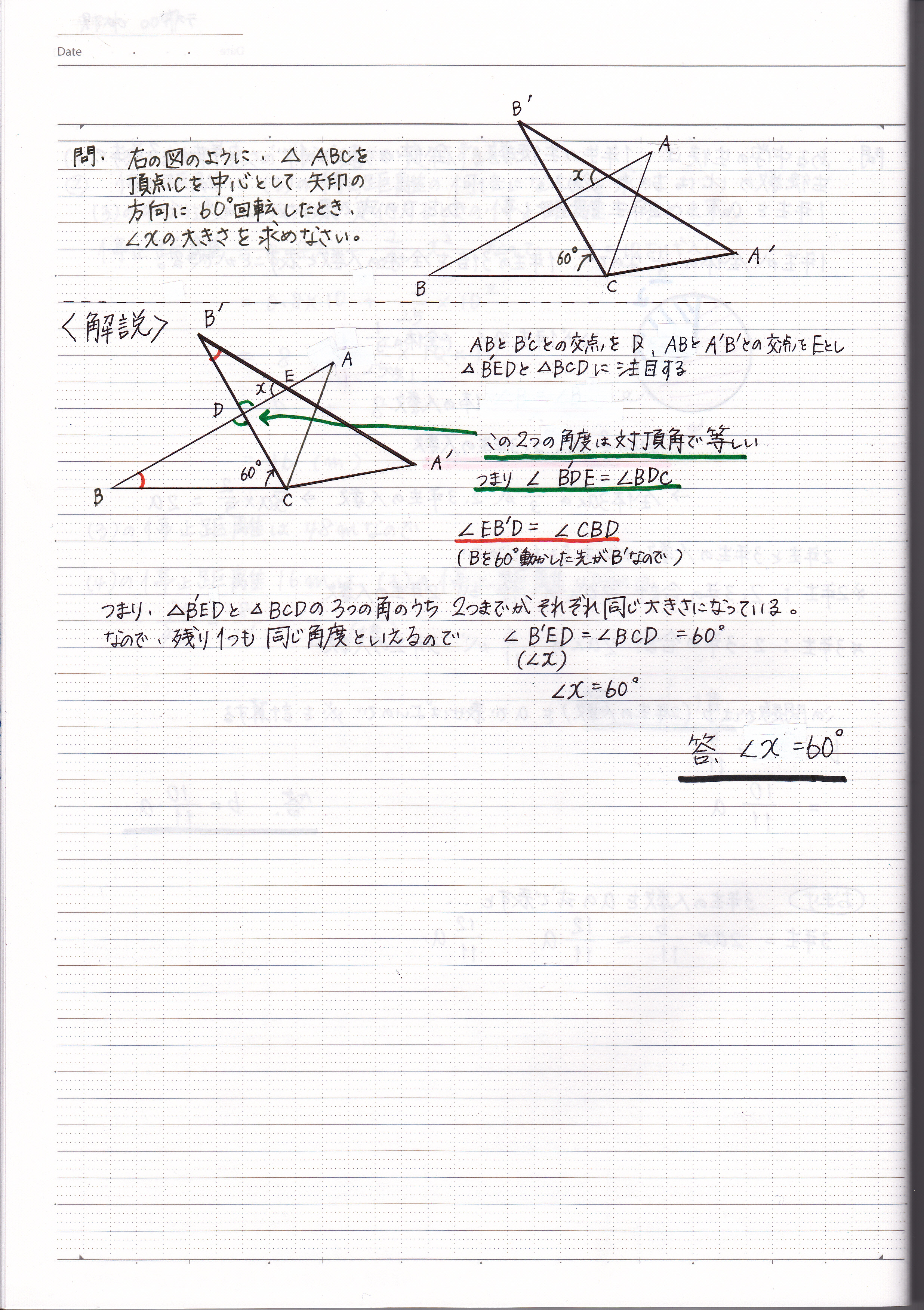



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
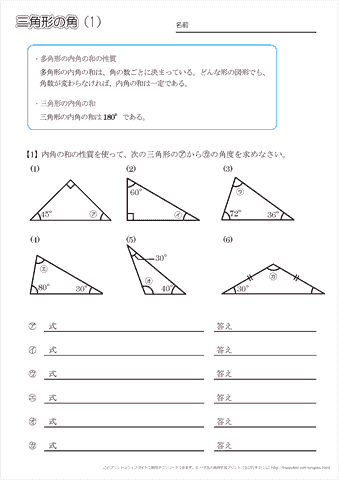



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
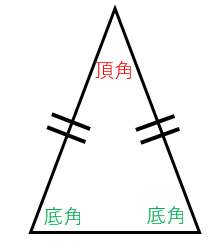



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学




高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト
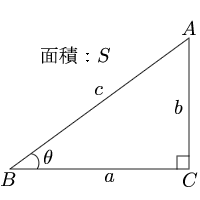



これまでで最高の三角形 の 底辺 子供のための最高のぬりえ



0 件のコメント:
コメントを投稿