Use graphical methods to solve the linear programming problem Maximize z = 6x 7y subject to 2x 3y ≤ 12 2x y ≤ 8 x ≥ 0 y ≥ 0 A) Maximum of 24 when x = 4 and y = 0 B) Maximum of 32 when x = 2 and y = 3 C) Maximum of 32 when x = 3 and y = 2 D) Maximum of 52 when x = 4 and y = 4 Answer by jim_thompson5910() (Show Source)1) xy = 3 2) xy = 5 First solve the equations for y 1) xy = 3 Subtract x from both sidesy = x3 Now multiply both sides by 1 to make the y positive y = x3 2) xy = 5 Subtract x from both sides y = x5 Now the graph From the graph, you can see that the two lines intersect at the point (4, 1) and this is the solution to the system ofAnswer (1 of 4) Using elimination 2x 3y = 5 ———(1) 4x—7y = —3 ———(2) Multiply eq (1) by 4 and eq (2) by 2 8x 12y = ———(3) 8x—14y = —6 ———(4) 26y = 26 Divide both sides by 26 y = 1 Substitute 1 for y in eq (1) 2x 3(1) = 5 2x 3 = 5 2x = 5—3 2x = 2 divide both sides by 2 x

Answers
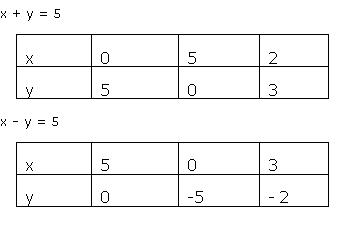
X y=5 x-y=3 graphical method
X y=5 x-y=3 graphical method-Elimination Method Steps Step 1 Firstly, multiply both the given equations by some suitable nonzero constants to make the coefficients of any one of the variables (either x or y) numerically equal Step 2 After that, add or subtract one equation from the other in such a way that one variable gets eliminatedNow, if you get an equation in one variable, go to Step 3Solve by Graphing xy=3 , xy=5, Subtract from both sides of the equation Subtract from both sides of the equation Multiply each term in by Tap for more steps Multiply each term in by Multiply Tap for more steps Multiply by Multiply by Simplify each term Tap for more steps Multiply by Multiply




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula
Solve the simultaneous equations \(x y = 5\) and \(y = x 1\) using graphs To solve this question, first construct a set of axes, making sure there is enough room to plot the two graphs Ex 34, 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 SolvingSolve the simultaneous equations by using Graphical method x 3y = 7;
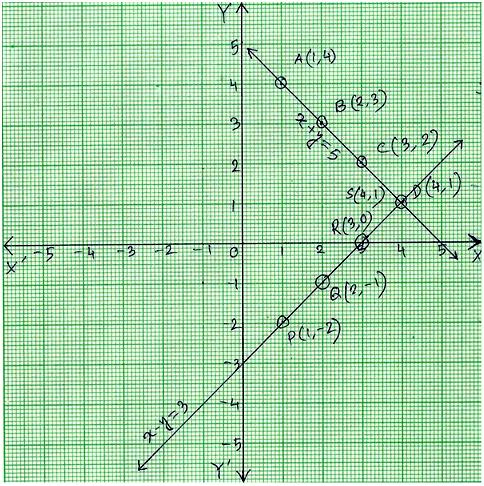
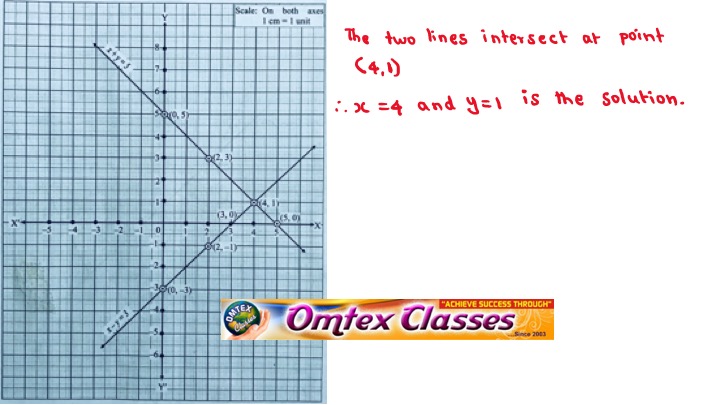
My native three this way of wise people 5/3 X minus five So it's drawing a graph that y intercept a negative five So for 5/3 with about 5/3 were down Five left, three No, in this other version we need is for track two acts so negative wise, Negative two x plus four about everything My negative one and so wise to x minus four You're wise toSubstitution Method xy = 5 and 2x3y = 4LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8ba/FaceBookhttps//wwwfacebookcom/arunkumarm144 multiplying (eq1) by 2 and subtracting (eq2) from ( eq1 ) (2x 2y = 10) (2x 3y = 4 ) => 2x 2y 2x 3y = 6 => 5y = 6 => y = 6/5 Putting the value of y in ( eq1 ) => x y = 5 => x 6/5 = 5 => x = 5 6/5
Y = 5 x y = 5 3 Therefore, we get the value ofIn this graphical method, the equations are designed based on the constraints and objective function To solve the system of linear equations, this method involves different steps to obtain the solutions Now substituting the value x = 3 in the other equation that is y = 5 – x, we get;Lesson 3 Graphical method for solving LPP Learning outcome 1Finding the graphical solution to the linear programming model Graphical Method of solving Linear Programming Problems Introduction Dear students, during the preceding lectures, we have learnt how to formulate a given problem as a Linear Programming model




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula
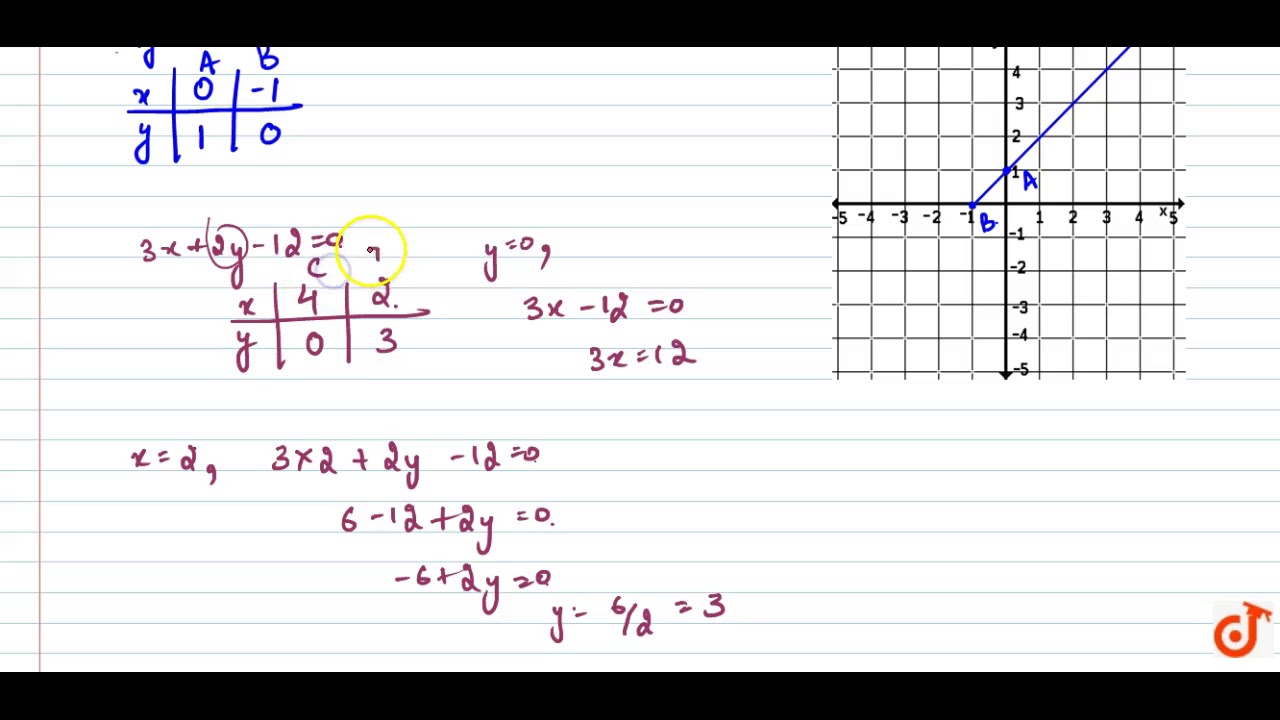



Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Determine The Coordinates Of The V Youtube
Minimize S x y= 2 7 subject to 5 5 3 9 0 0 x y x y x y ≥ ≥ ≥ ≥ Solution We need to graph the system of inequalities to produce the feasible set We will start by rewriting each inequality as an equation, and then number the equation for each line 5 5 (1) 3 9 (2) 0 (3) 0 (4) x y x y x y = = = =Solve the following LPP by graphical method Minimize Z = 7x y subject to 5x y ≥ 5, x y ≥ 3, x ≥ 0, y ≥ 0The Graphical Simplex Method An Example Consider the following linear program Max 4x1 3x2 Subject to 2x1 3x2 6 (1) 3x1 2x2 3 (2) 2x2 5 (3) 2x1 x2 4 (4) x1;



26 Free Simultaneous Equations Worksheets And Lesson Plans For Ks3 And Ks4 Maths



Ex 6 2 1 Solve X Y 5 Graphically Chapter 6 Ncert
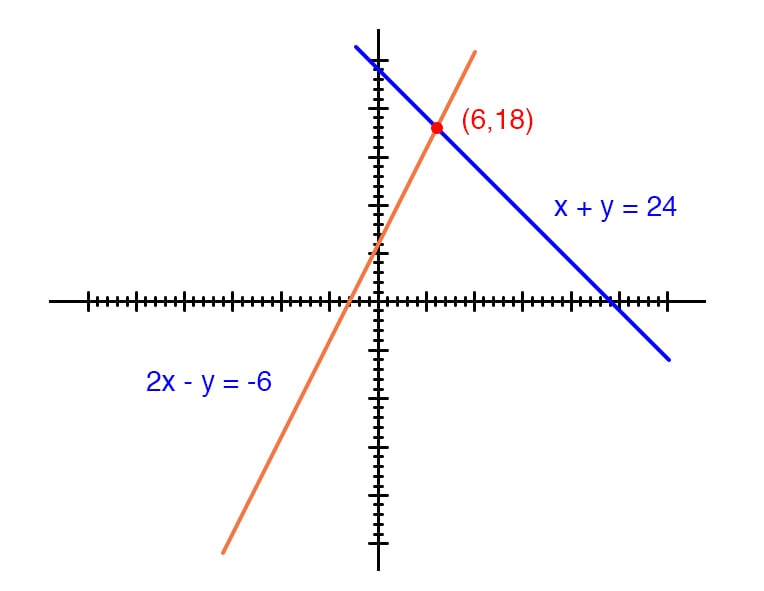
2x y 1 = 0 PDF FILE TO YOUR EMAIL IMMEDIATELY PURCHASE NOTES & PAPER SOLUTION @ Rs 50/ each (GST extra) HINDI ENTIRE PAPER SOLUTION MARATHI PAPER SOLUTION SSC MATHS I#SahajAdhyayan #सहजअध्ययन #graphicallyShare this video with your friends on WhatsApp, Facebook, Instagram, twitter You can also join us on all of those sociZ=X10Y Z=2410() Z=904=Maximum Optimal Solution Two Types of Linear Programming Simplex Method & Graphical Method There are two types of linear programming the simplex method and the graphical method The simplex method is a set of instructions used to find the optimal solution to multivariable problems The simplex method helps us "examine corner points



Systems Of Equations Graphical Method Video Lessons Examples Solutions




Solve Using Graphical Method 4x Y 6 And 3x 5y 16
Given linear equations are y = x 1 and x y = 5 On a graph paper to solve simultaneous equations graphically, draw a horizontal line X'OX and a vertical line YOY' as the xaxis and yaxis respectively The first equation y = x 1 is in the slope intercept form y = mx c m = 1, c = 1 Now apply the trial and error method to get the 3 pairs of points (x, y) which satisfy2x – y = 4 Solution Given x y = 5 (1) 2x – y = 4 (2) To draw the graph (1) is very easy We can find the x and y values and thus two of the points on the line (1) When x = 0, (1) gives y = 5 Thus A(0,5) is a point on the line When y = 0, (1) gives x = 5Part 3 Determination of X and Y Components of a Force Table 3A Graphical Method Solution (Scale 102 g = 1 cm*, dm = 1 g, dl = 1 mm, dq = 1°)



1



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook
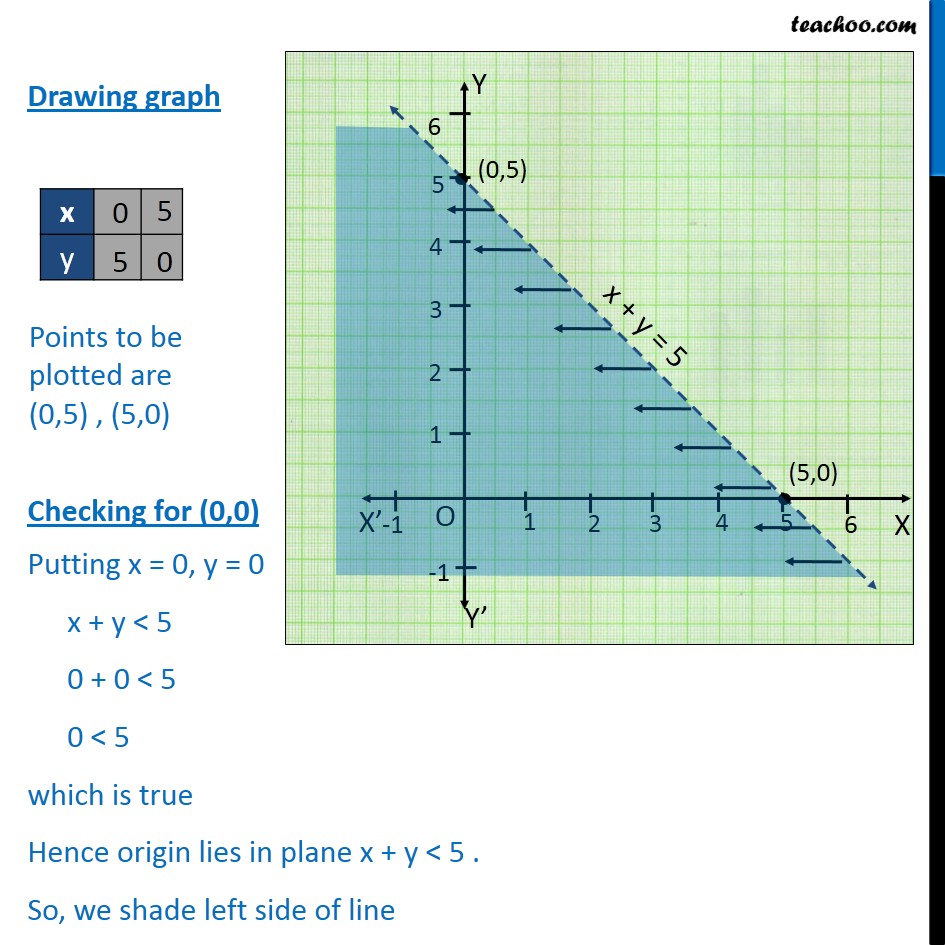
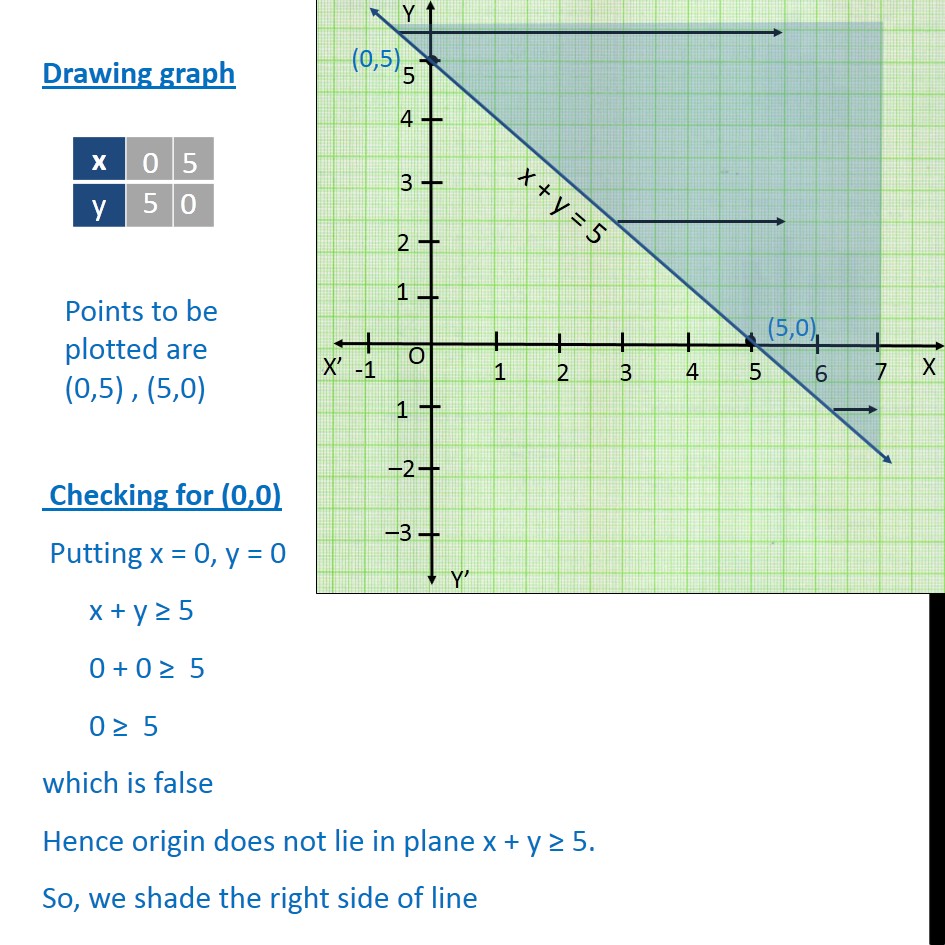
So, we shade the right side of line Now we solve x – y ≤ 3 Lets first draw graph of x – y = 3 Drawing graph Checking for (0,0) Putting x = 0, y = 0 x – y ≤ 3 0 – 0 ≤ 3 0 ≤ 3 which is true Hence origin lies in plane x y ≥ 5 So, we shade left side of line Hence the shaded region is the solution of the given inequalityNow, we find the point of intersection of these lines to find the values of 'x' and 'y' The two lines intersect at the point (3,5) Therefore, x = 3 and y = 5 by using the graphical method of solving linear equations Let us look at one more method of solving linear equations, which is the cross multiplication method When, x = 2, y = –3 × 2 11 = 5 When, x = 3, y = – 3 × 3 11 = 2 Plotting the points P (2, 5) and Q(3, 2) on the graph paper and drawing a line joining between them, we get the graph of the equation 3x y – 11 = 0 as shown in fig (b) Graph of the equation x – y – 1 = 0 We have, x – y – 1 = 0 y = x – 1 When, x = – 1, y = –2 When, x = 3, y = 2




Draw The Graph Of Following Equation X Y 5 X Y 5 Find The Solution Of The Equation From Brainly In



Graph Graph Equations With Step By Step Math Problem Solver
A a = 0, b = 0 b a = 3, b = 3 c a = 0, b = 6 d a = 6, b = 0 e cannot solve without values for a and b c a = 0, b = 6 A maximizing linear programming problem has two constraints 2X 4Y < 100 and 3X 10Y < 210, in addition to constraints stating that both X and Y must be nonnegative The corner points of the feasible region of thisExample (part 2) Graphical method Initially the coordinate system is drawn and each variable is associated to an axis (generally 'x' is associated to the horizontal axis and 'y' to the vertical one), as shown in figure 1 A numerical scale is marked in axis, appropriate to the values that variables can take according to the problem constraints 5 Graphical Solution of nonLinear Systems A nonlinear graph is a curve This section assumes you already know the formulas for straight lines, circles, parabolas, ellipses and hyperbolas You can refresh your memory in the Plane Analytic Geometry chapter In this section, we see how to solve nonlinear systems of equations (those involving



Simultaneous Equations Graphically Solve Graphically The System Of Equations




Draw The Graphs Of The Following Equations X Y 5 X Y 5 I Find The Solution Of The Equations From The Graph Ii Shade The Triangular Region Formed By Th Mathematics Topperlearning Com Rmtc0aktt
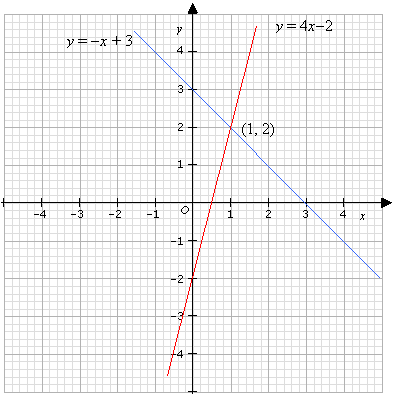
Y = 2 x – 2 The first equation is x 2y = 5 x 1 3 5 y 2 1 0 (x,y) (1,2) (3,1) (5,0) Now the second equation is y = 2 x – 2 x 1 2 0 y462 (x,y) (1, 4) (2, 6) (0, 2) The Point of intersection is ( 3 , 4) Email This BlogThis!Using the graphical method, find the solution of the systems of equations y x = 3 y = 4x 2 Solution Draw the two lines graphically and determine the point of intersection from the graph From the graph, the point of intersection is (1, 2)The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first



Omtex Classes X Y 5 X Y 3 Solve The Following Simultaneous Equations Graphically
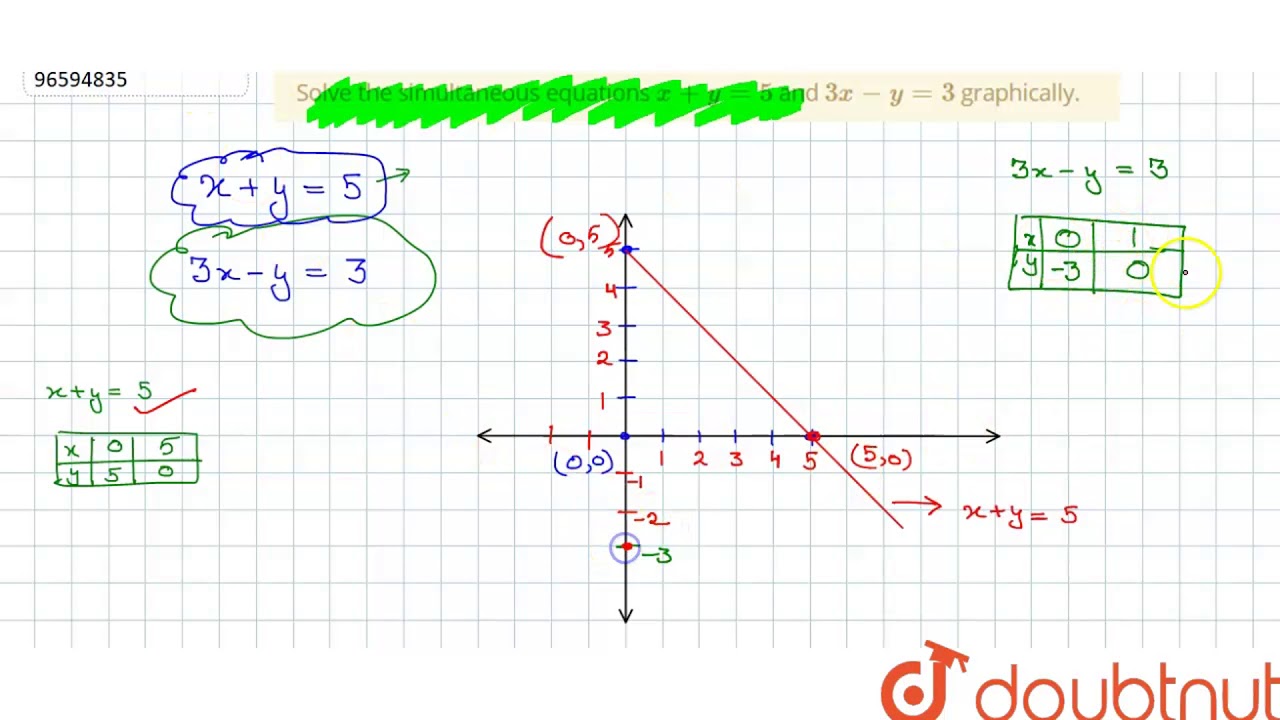



Solve The Simultaneous Equations X Y 5 And 3x Y 3 Graphically Youtube
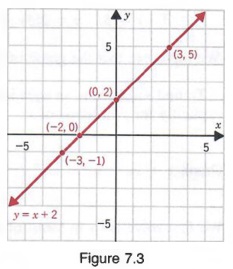
2x y = 32 x 3y = 36 8 ≟ 32 12 31 ≟ 36 32 = ˜32 36 = 36 Check that 112, satisfies each of the original equations Matched Problem 1 Solve by graphing and check 2xy = 3 x 2y = 4 It is clear that Example 1 has exactly one solution since the lines have exactly one point in a 1 x b 1 y c 1 = 0 a 2 x b 2 y c 2 = 0 In this crossmultiplication method, The solution is given by, Question 1 Solve the following equations with the elimination method 2x 3y = 46 3x 5y = 74 Solution a 1 = 2, a 2 = 3, b 1 = 3, b 2 = 5, c 1 = 46 and c 2 = 74 x = 8 and y = 10 Question 2 Solve the following pair of equationsWe designate (3, 5) as (x 2, y 2) and (4, 2) as (x 1, y 1) Substituting into Equation (1) yields Note that we get the same result if we subsitute 4 and 2 for x 2 and y 2 and 3 and 5 for x 1 and y 1 Lines with various slopes are shown in Figure 78 below
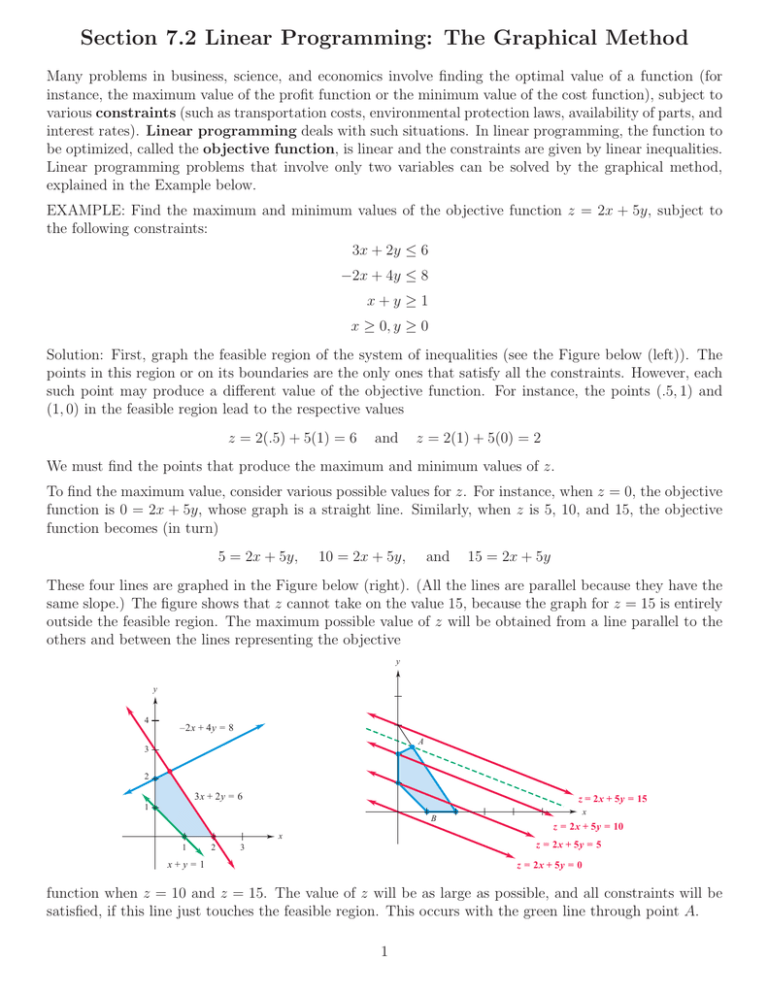



Section 7 2 Linear Programming The Graphical Method




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper
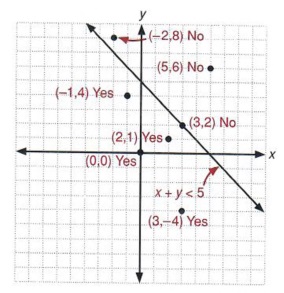
Solve the equations 2 x 2 y = 4 and − 2 x 3 y = 1 using graphical method Medium View solution Using graphical method check whether the given equation is consistent 2 x 3 y = 8 and 3 x 6 y = 1 5 Medium View solution View more Learn with content Watch learning videos, swipe through stories, and browse through conceptsObserve that all "yes" answers lie on the same side of the line x y = 5, and all "no" answers lie on the other side of the line or on the line itself The graph of the line x y = 5 divides the plane into three parts the line itself and the two sides of the lines (called halfplanes) x y 5 is a halfplane x y 5 is a line and a halfplaneOverdetermined System for a Line Fit (2) Writing out the αx β = y equation for all of the known points (x i,y i), i =1,,mgives the overdetermined system 2 6 6 4 x1 1 x2 1 x m 1 3 7 7 5 » α β – = 2 6 6 4 y1 y2 y m 3 7 7 5 or Ac = y where A = 2 6 6 4 x1 1 x2 1 x m 1 3 7 7 5 c = α β – y = 2 6 6 4 y1 y2 y m 3 7 7 5 Note We cannot solve Ac = y with Gaussian elimination Unless the



Systems Of Linear Equations




X Y 5 X Y 3 Simultaneous Equation Graphically Brainly In
X2 0 Goal produce a pair of x1 and x2 that (i) satis es all constraints and (ii) has the greatest objectivefunction valueExample 344 Use graphical method to solve the following system of equations x y = 5;Solve the following simultaneous equations using graphical method x 2 y = 5;



Solve Graphically I X Y 7 X Y 3 Scholr
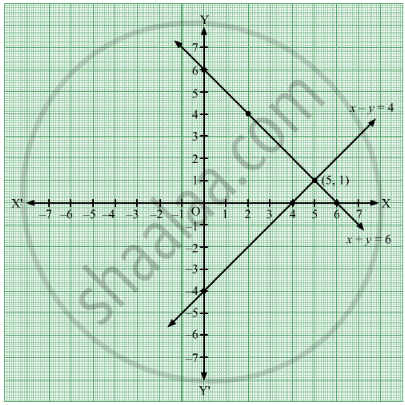



Solve The Following Simultaneous Equations Graphically X Y 6 X Y 4 Algebra Shaalaa Com
Click here👆to get an answer to your question ️ Solve the given simultaneous equations using graphical method x y = 5,x y = 3 By plotting each of those equations, you will get two straight lines which intersect at the point (3,4) That means that both equations are true when x=3 and y=4 Graphically, the solution to this system of equations is (3,4)1 and substitute the numbers a and b for the values of x and y in the given inequality For simplicity, use the origin, (0,0), whenever possible 3 If the inequality is satisfied (True), the graph of the solution to the inequality is the halfplane containing the test point (Shade the region containing the test point) Otherwise (if the inequality




Solved 1 Solve The Following Using Graphical Method 12 Chegg Com




Draw The Graph Of The Following Equations X Y 5 X Y 5 And Find The Solution From The Graph Also Maths Pair Of Linear Equations In Two Variables Meritnation Com
Our online system of equations calculator helps you to solve for any unknown varriables x,z, n, m and y The simultaneous equation calculator above will help you solve simultaneous linear equations with two, three unknowns A system of 3 linear equations withExamples_Graphical__simplex_2pdf graphical method and simplex method Section one Example(1 Min(x y =2x y x 2y \u2264 16 3x 2y \u2264 12 x y \u2264 0 SolveObjective function Max Z = 100 x 80 y Subjected to constraints 5x 3y ≤ 150 x y ≤ 40 Shaded region is the feasible region Finding the corner points coordinates of B As B is intersection of x y = 40 5x 3y = 150 On solving these coordinates of B is (15, 25) Now, finding value of objective function at all corner points Z(A




Mex 4 5 Nmax Maxita In Poblen 3 R Y S1 4 X S35 5 Chegg Com




Solve The Equation Graphically X Y 7 X Y 3 Brainly In
\x = 1,\;y = 3\ 3 Graphical Method As an example, consider the following pair of linear equations \\begin{array}{l} x y = 0\\ x y 4 = 0\end{array}\ We draw the corresponding lines on the same axes Introduction to graphical & numerical methods A linear equation containing variables 'x' and 'y' is of the form ax by c = 0, it represents a straight line So, the problem of solving two simultaneous linear equations with variables 'x' and 'y' reduces to the problem of finding the common point between theFree system of equations calculator solve system of equations stepbystep



Draw The Graphs Of The Following Equations X Y 5 X Y 5 I Find The Solution Of The Equations From The Graph Ii Shade The Triangular Region Formed By Th Mathematics Topperlearning Com Rmtc0aktt



How To Solve For X And Y In X Y 5 And Xy 6 Quora
Example 1 Use a graph to solve the simultaneous equations Now draw the graphs y = – x and y = x – 2 The lines cross at the point with coordinates (11, 9), so the solution of the pair of simultaneous equation is x = 11, y = 9 Note this means that the solution to the problem presented at the start of section 55 is that Claire is aged




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula




Solve The Given Simultaneous Equations Using Graphical Method X Y 5 X Y 3




Teaching X And Y Axis Graphing On Coordinate Grids Houghton Mifflin Harcourt




Solve The Following System Of Linear Equations Graphically 2x Y 6 X 2y 2 0 Find The Vertices Of The Triangle Formed By The Above Two




Solved 2 3 Consider The Region Bounded By Y 5 X Y 2x Chegg Com
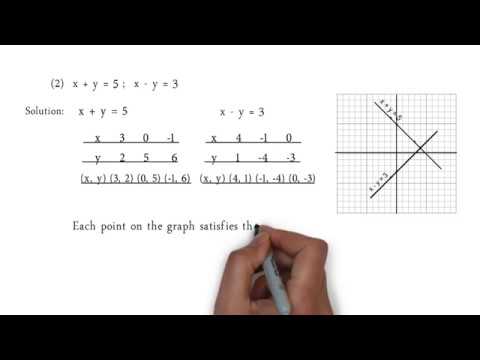



X Y 5 And X Y 3 P S 1 2 Q2 2 Linear Equations In Two Variables Youtube
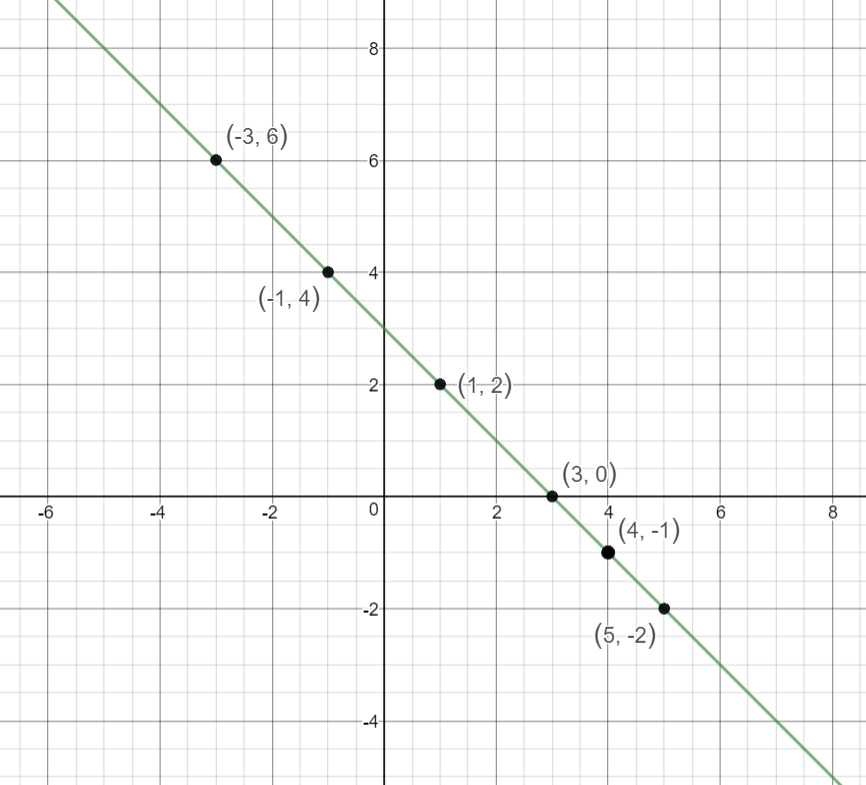



How Do You Graph X Y 3 By Plotting Points Socratic




2 X Y 3 X Y 1 8 X Y 7 X Y 5 6 Solve X And Y Youtube




Graph Of X Y 7 X Y 3 Brainly In




Use Graphical Method To Solve The Following Systems Of Equation X Y 5 2x Y 4 Brainly In




X Y 5 X Y 3 Solve The Simultaneous Equation Graphically Brainly In




Graphing A Linear Equation 5x 2y Video Khan Academy




Draw Graph For X Y 5 X Y 8 Brainly In



Example 12 Solve X Y 5 X Y 3 Graphically Examples




Example 12 Solve X Y 5 X Y 3 Graphically Examples




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper




X Y 7 X Y 5 Graphical Equation Brainly In



2




Draw The Graph Of Line X Y 5 Use The Graph Paper Drawn To Find The Inclination And The Y Intercept Of The Line




Solved Solve The Graphical Method The Following System Of Chegg Com




How Do You Solve The System 4x 2y 6 And X Y 3 Socratic




Answers
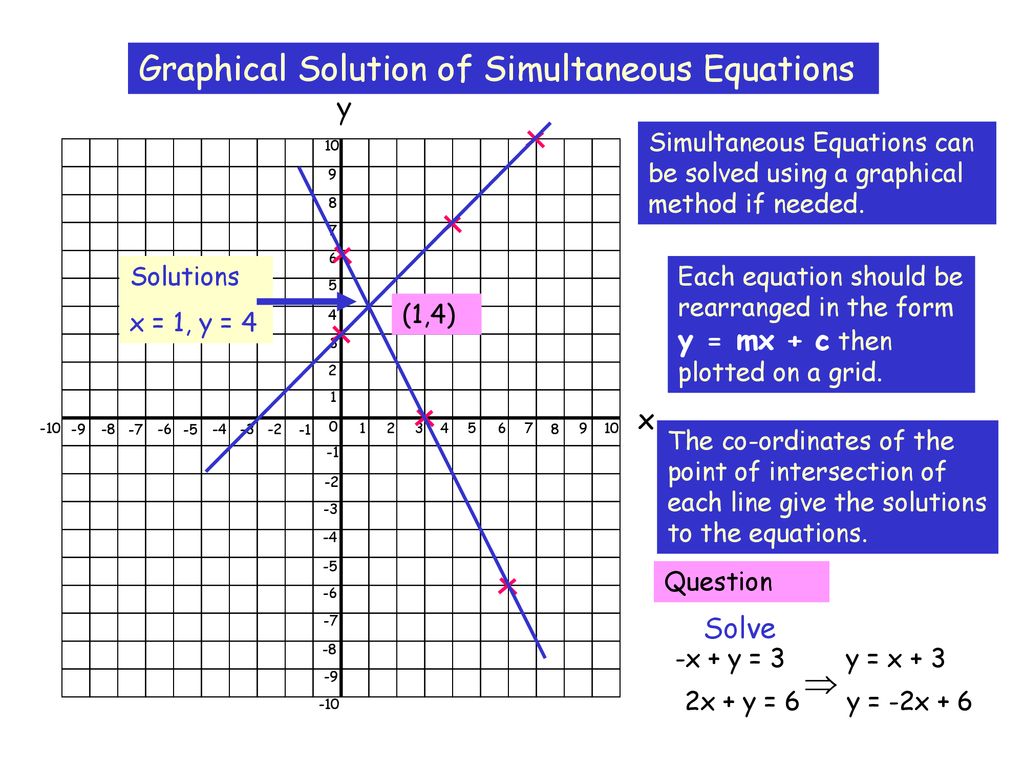



Graphical Solution Of Simultaneous Equations Ppt Download




Omtex Classes X Y 5 X Y 3 Solve The Following Simultaneous Equations Graphically




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula
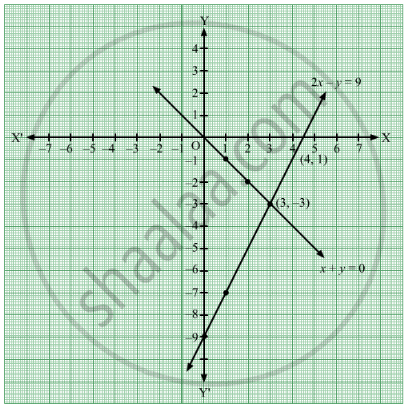



Solve The Following Simultaneous Equations Graphically X Y 0 2x Y 9 Algebra Shaalaa Com




Graph Linear Equations In Two Variables Elementary Algebra
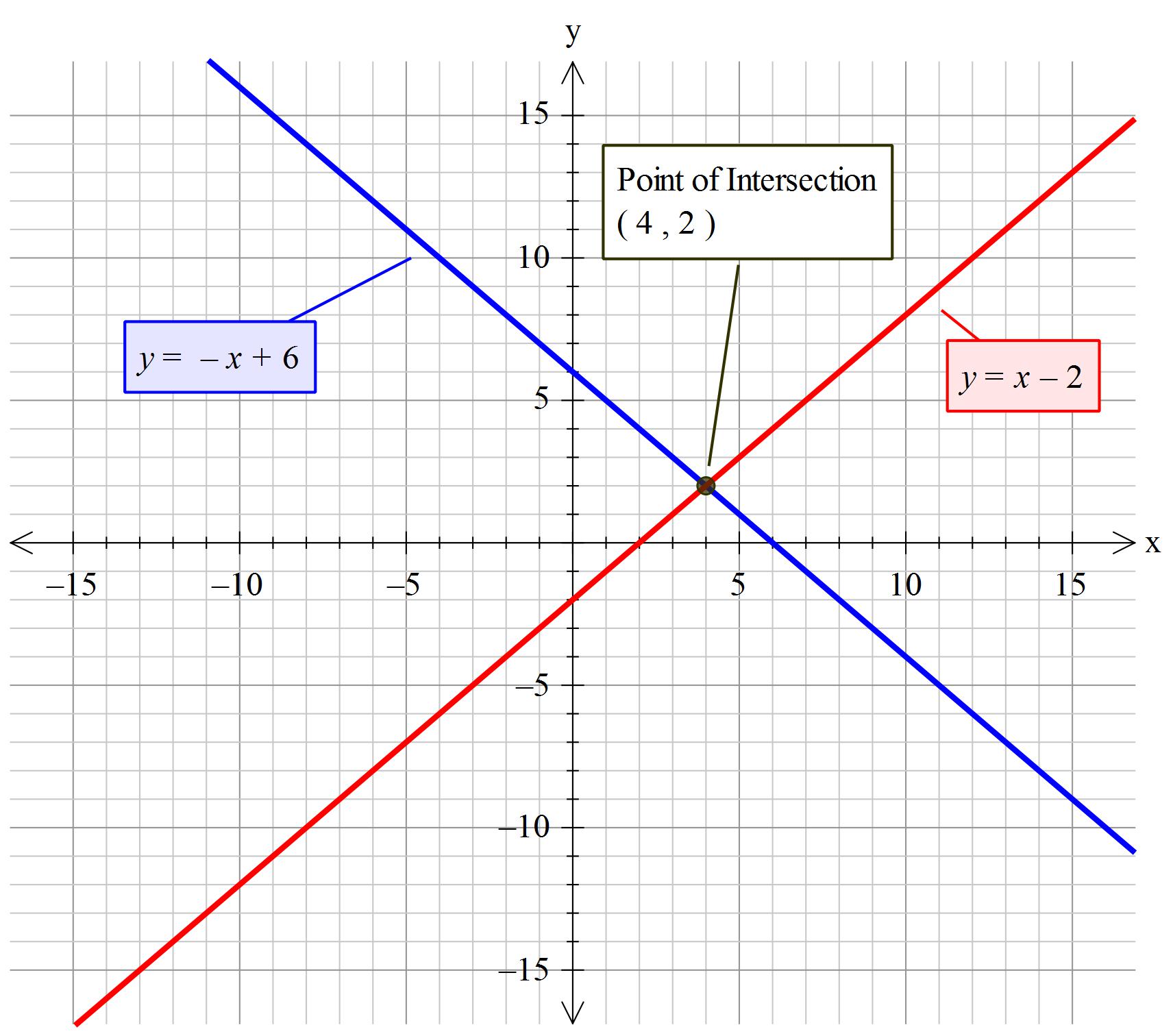



How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic




How To Solve Equation X Y 3 And X Y 4 By Graphical Method Maths Linear Equations In Two Variables Meritnation Com




Solve An Equation Graphically X Y 3 X Y 1 Brainly In
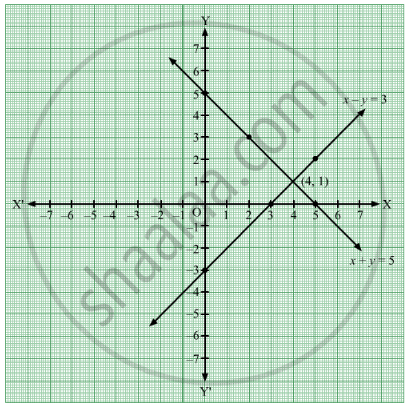



Solve The Following Simultaneous Equations Graphically X Y 5 X Y 3 Algebra Shaalaa Com




Ex 6 2 1 Solve X Y 5 Graphically Chapter 6 Ncert
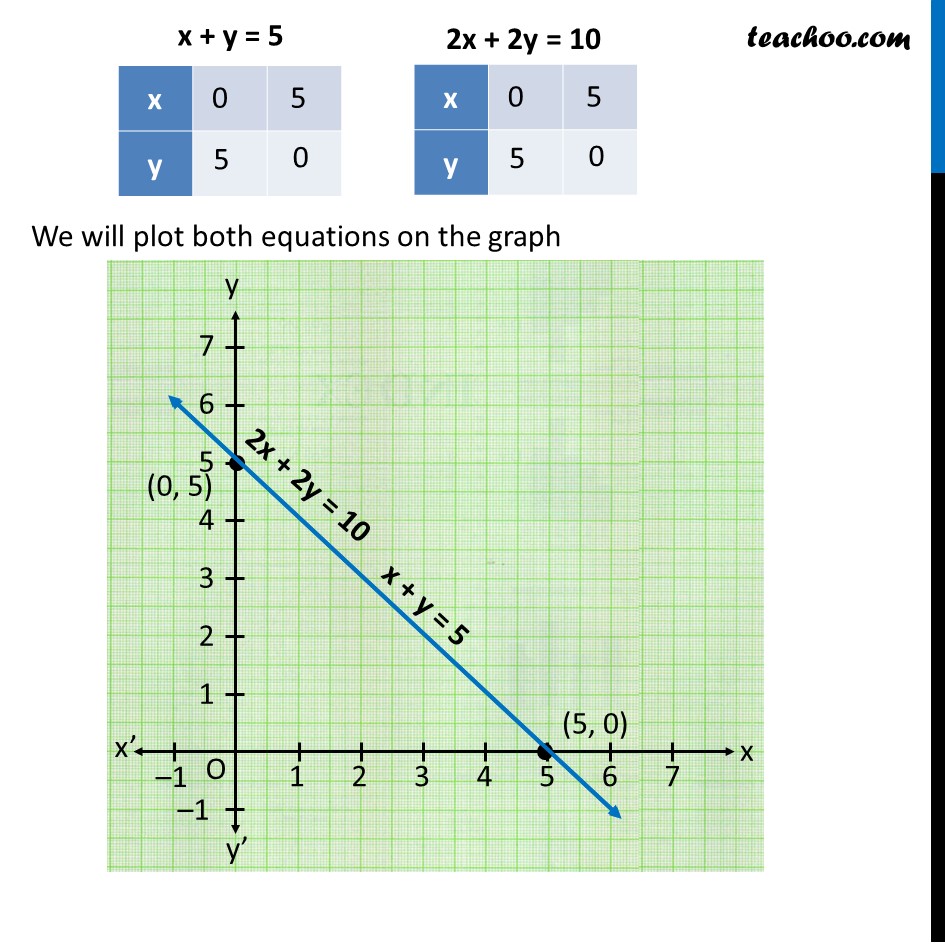



Ex 3 2 4 I Which Of The Pairs Of Linear Equations Are Consistent




Solve The Following Pair Of Linear Equations Using Graphical Method X Y 8 X Y 2 Then X Y Is Equal To




Solved Ie 222 Homework 1 Graphical And Simplex Method Chegg Com



Simultaneous Equations Graphically Solve Graphically The System Of Equations



Graphical Solution Of Simultaneous Linear Equations Youtube
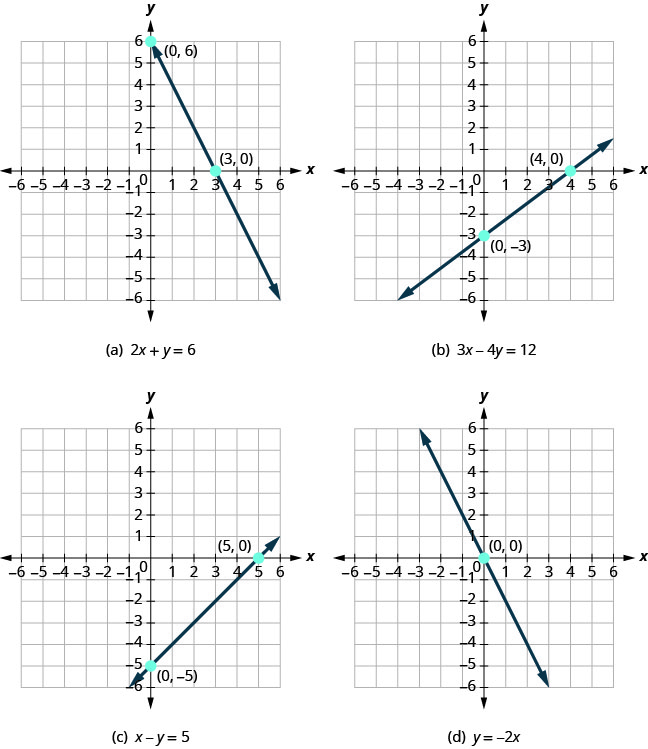



Graph With Intercepts Elementary Algebra



Graphing Linear Inequalities




Solve The Given Simultaneous Equations Using Graphical Method X Y 5 X Y 3 Brainly In




Draw The Graph Of Equation X Y 7



Solution I Have To Solve Utilizing The Graphing Method X Y 3 X Y 5




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper



How Do You Solve The System Of Equations X Y 3 And 3x 2y 14 By Graphing Socratic



Solve The Following Systems Of Equations Graphically 2x 3y 4 X Y 3 0 Sarthaks Econnect Largest Online Education Community
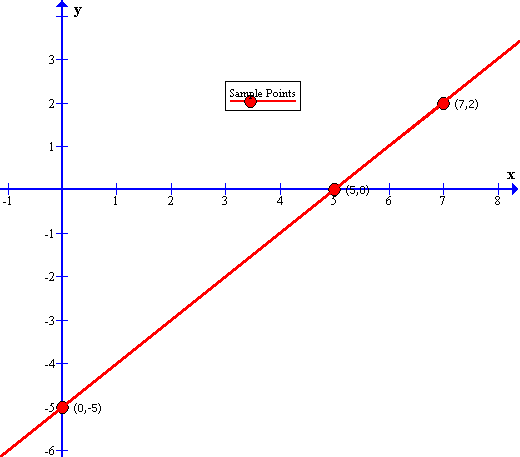



How Do You Graph The Line X Y 5 Socratic
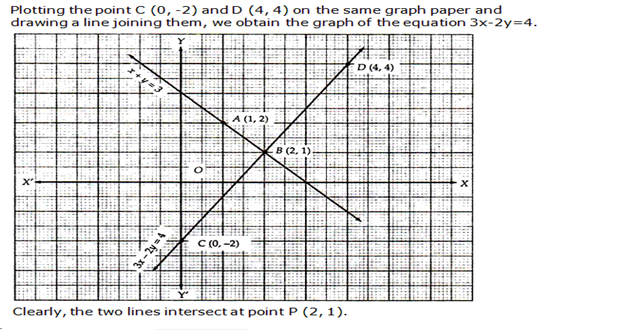



Solve Graphically The System Of Equations X Y 3 3x 2y 4 Mathematics Topperlearning Com Ja91bwemm




Show Graphically That The Given System Of Equations 2x 4y 10 And 3x 6y 12 Has No Solution



Simultaneous Equations Graphically Solve Graphically The System Of Equations
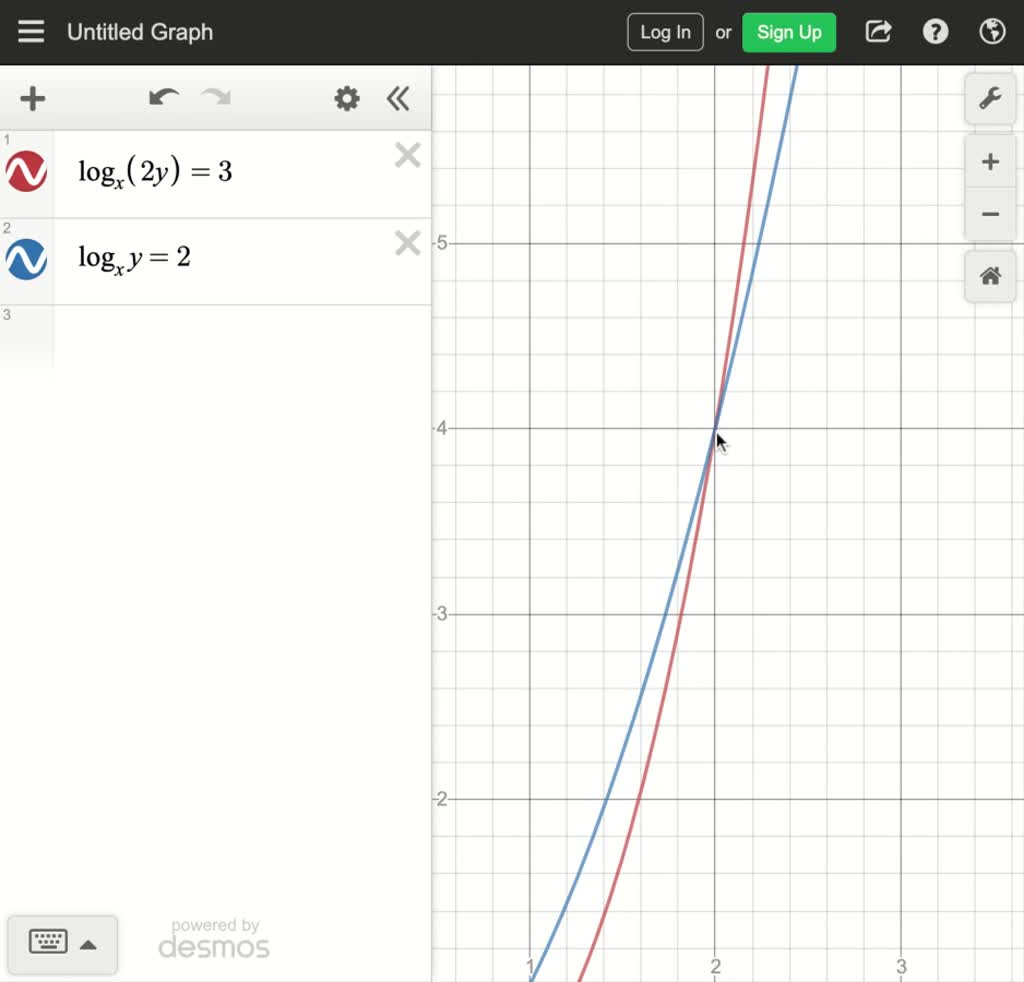



Solved Solve The System Use Any Method You Wish Log X Y 3 Log X 16y 5
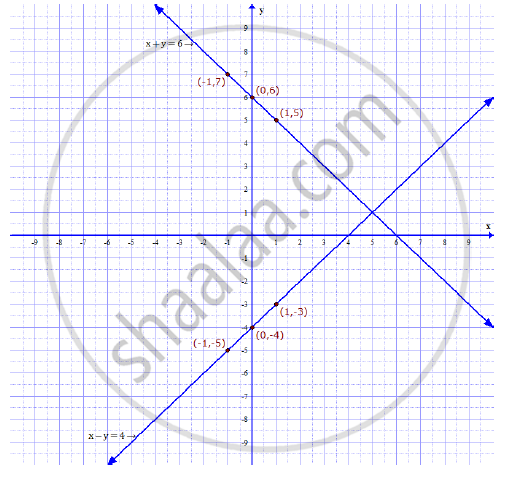



Solve The Following Simultaneous Equations By Using Graphical Method X Y 6 X Y 4 Algebra Shaalaa Com
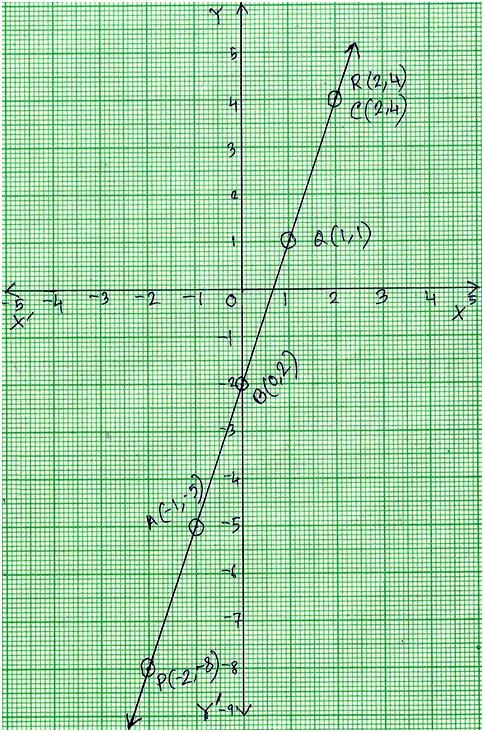



Simultaneous Equations Graphically Solve Graphically The System Of Equations




Slove The Substitution Method X Y 5 X Y 1 Brainly In




How To Graph X Y 3 Youtube
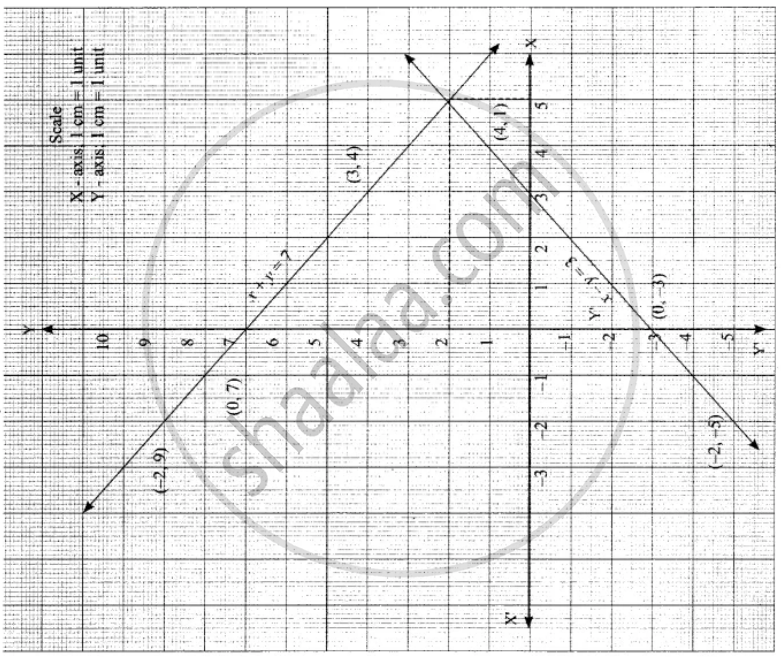



Solve Graphically X Y 7 X Y 3 Mathematics Shaalaa Com



2
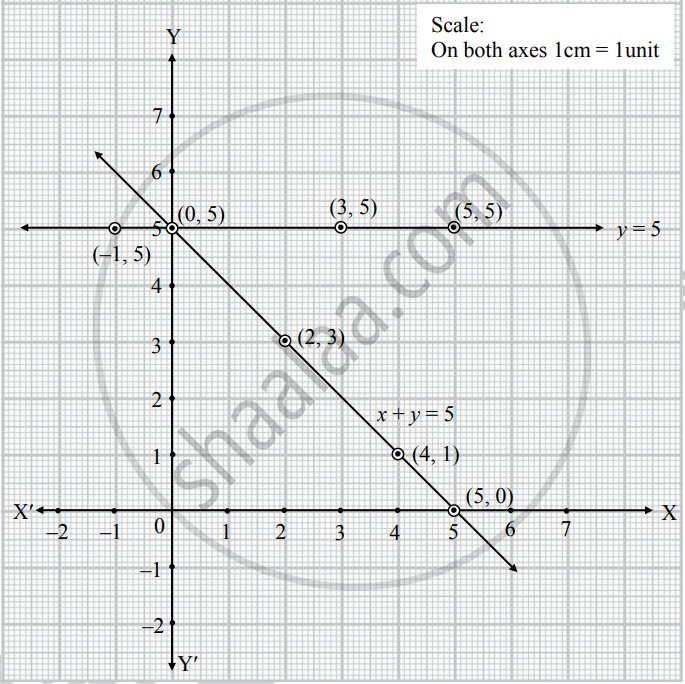



Solve The Given Simultaneous Equations Graphically X Y 5 And Y 5 Algebra Shaalaa Com



10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube
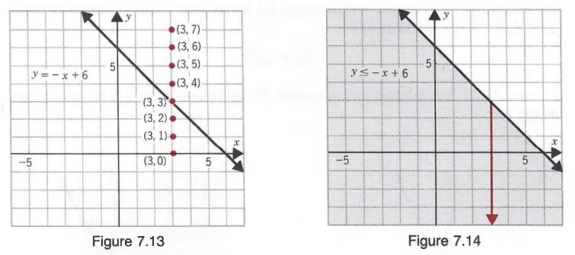



Graph Graph Equations With Step By Step Math Problem Solver
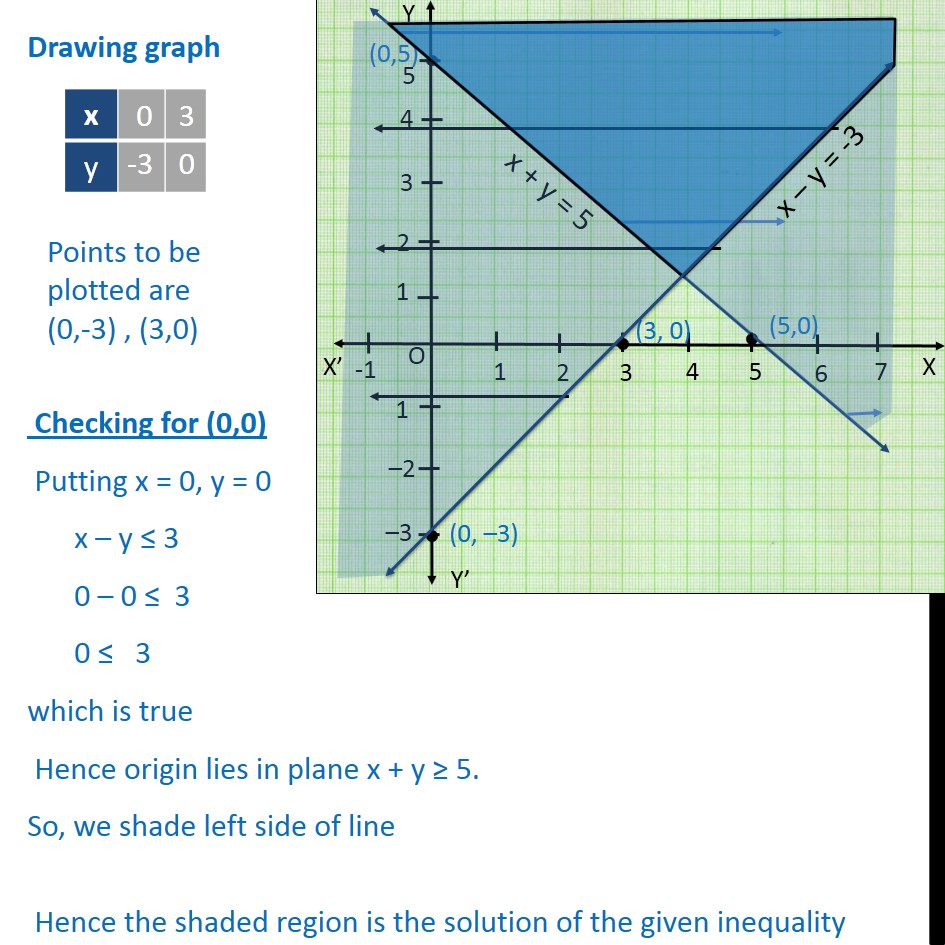



Example 12 Solve X Y 5 X Y 3 Graphically Examples
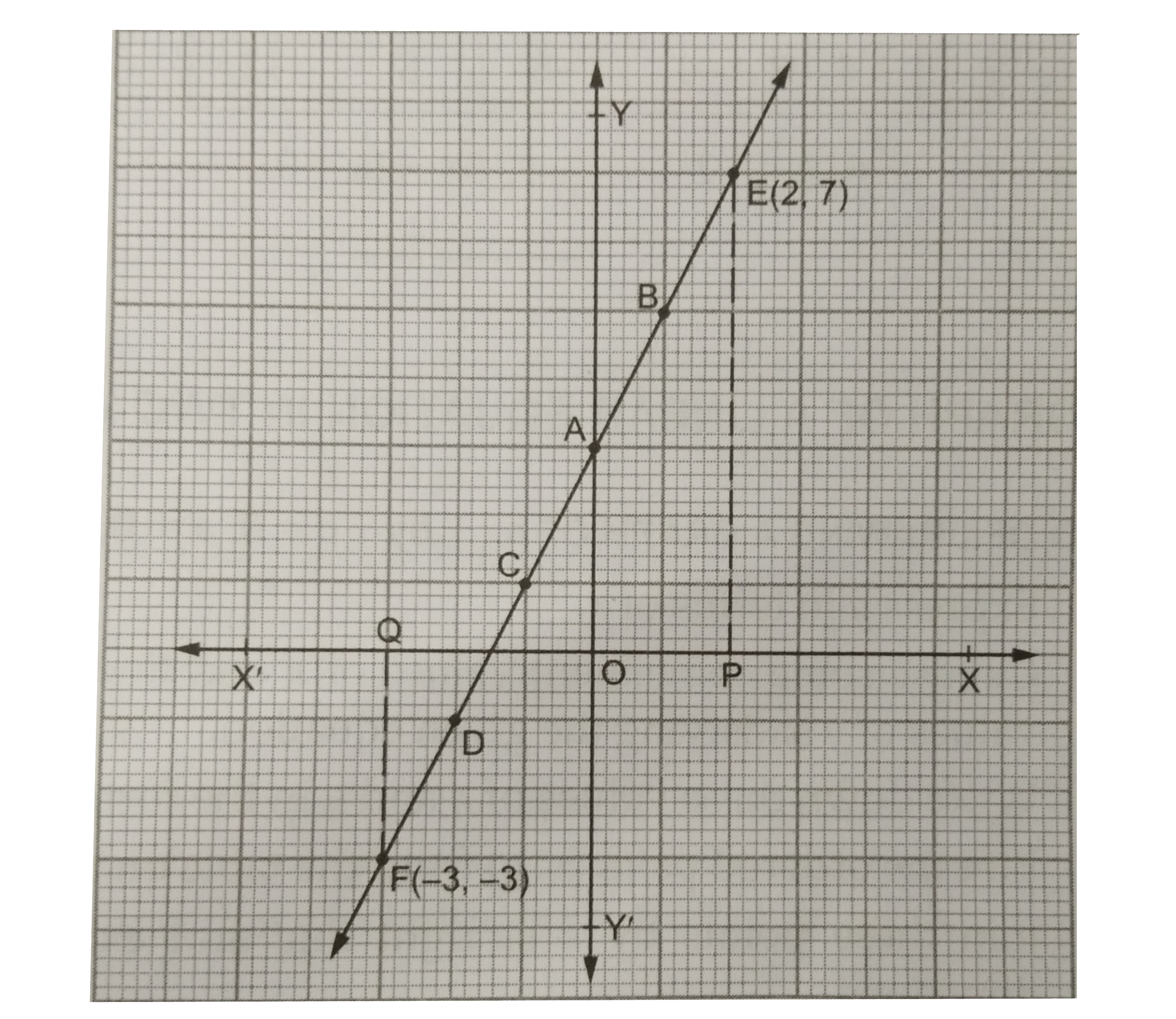



Draw The Graph Of The Equation 2x Y 3 0 Using The Graph Find The Value Of Y When A X 2 B X 3



Solution Solve Each System Grahpically X Y 5 X Y 1




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation




Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy




Ex 3 2 4 I Which Of The Pairs Of Linear Equations Are Consistent
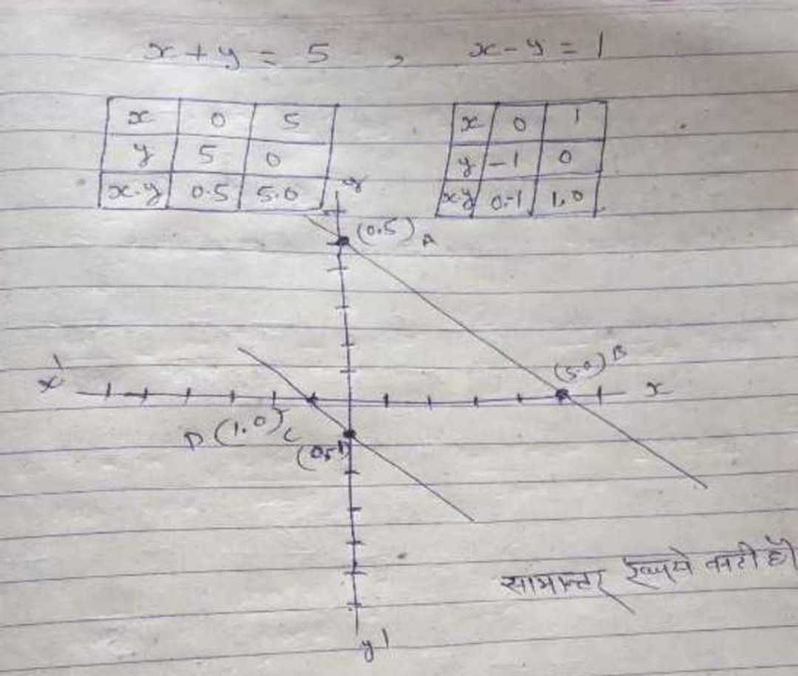



Solve Graphically X Y 5 And X Y 1 Scholr
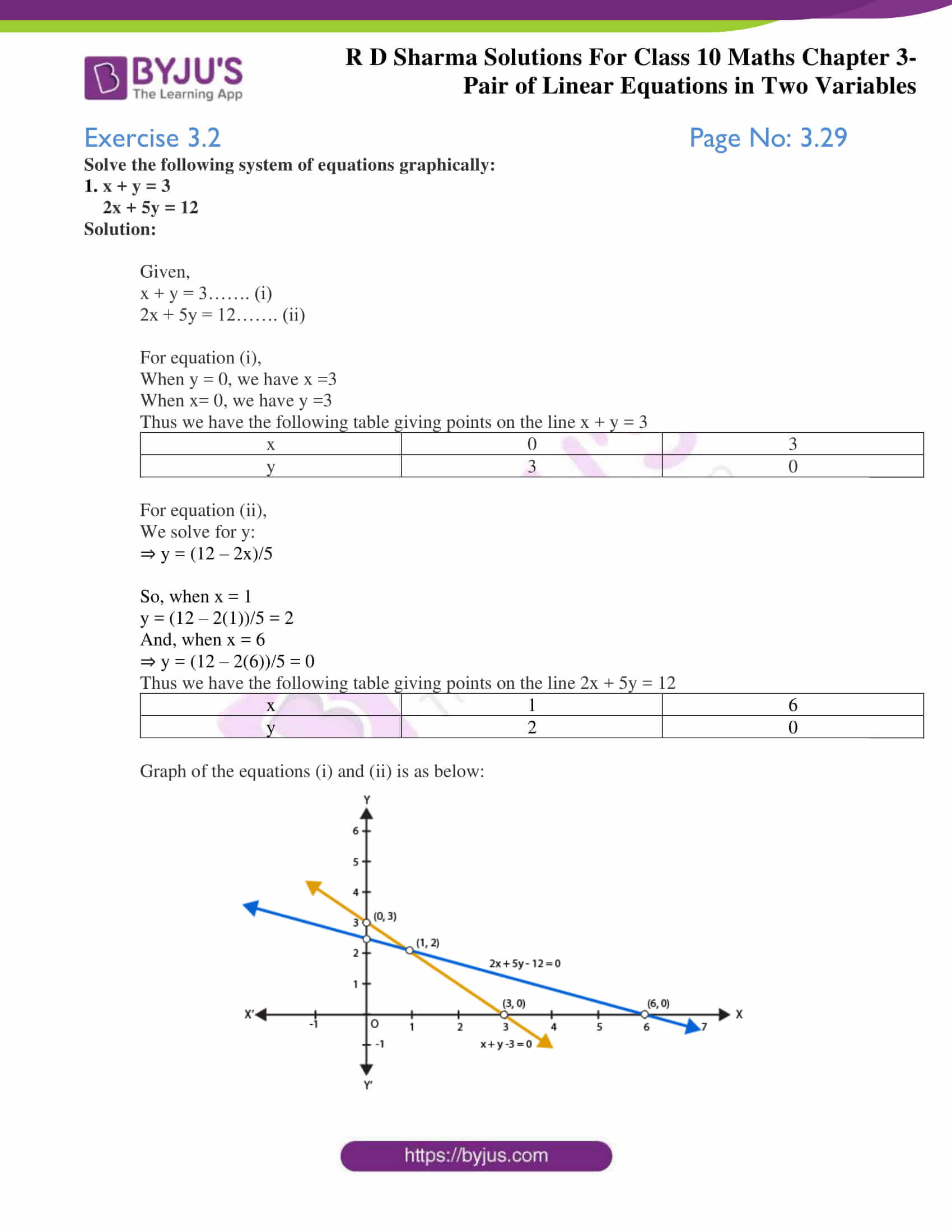



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




X Y 5 X Y 3 Practice Set 1 2 Simultaneous Equation Graphically आल ख पद धत Graphical Method Youtube



Graph Graph Inequalities With Step By Step Math Problem Solver



How To Solve X Y 7 And X Y 1 Graphically Quora




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation




Solved Med X Y 3 3x 4y 12 1 Solve By Graphing Mobis Chegg Com



1




X Y 5 X Y 3 Practice Set 1 2 Simultaneous Equation Graphically आल ख पद धत Graphical Method Youtube




Graph Graph Inequalities With Step By Step Math Problem Solver



Equation




Solve Graphically The System Of Equations X Y 3 3x 2y 4 Mathematics Topperlearning Com Ja91bwemm



0 件のコメント:
コメントを投稿